搜索
【题目】先阅读下列段文字，再解答问题：
已知在平面内有两点
其两点间的距离公式为：
（1）已知点P（2，4）、Q（-3，-8），试求P、Q两点间的距离；
（2）已知点A（0，6）、B（-3，2）、C（3，2），判断线段AB、BC、AC中哪两条线段是相等的？并说明理由；
（3）已知点
且MN=10，求
的值．
参考答案：
【答案】（1）13；（2）AB=AC；（3）m=8或－4．
【解析】
（1）根据两点间的距离公式计算；
（2）分别求出AB，AC，BC，即可得到结论；
（3）根据两点间的距离公式列方程，求解即可．
（1）∵P（2，4）、Q（-3，-8），，∴PQ
=
=13；
（2）∵AB=
=
=5，BC=
=6；AC=
==5，∴AB=AC．
（3）MN=
=10，∴
，∴m-2=±6，解得：m=8或－4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。
(1)如图2所示,求
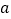的值；(2)如图3所示:
①若
求整式D；②若
求这九个整式的和是多少。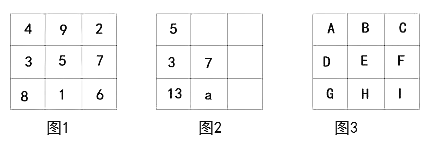
-
科目： 来源： 题型：
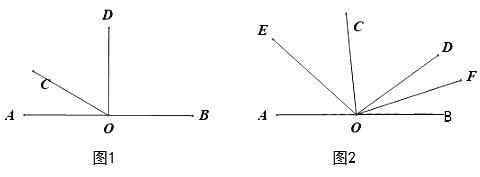
查看答案和解析>>【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数；
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2，OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小；若改变,说明理由；
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD，多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=﹣x2+2x+2
（1）求该抛物线的对称轴、顶点坐标以及y随x变化情况；
（2）在如图的直角坐标系内画出该抛物线的图象．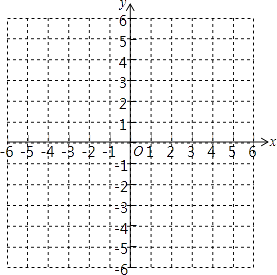
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1=∠2，则下列条件中不一定能使△ABC≌△ABD的是( )
A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．
（1）若∠CBD=39°，求∠BAD的度数；
（2）求证：∠1=∠2． -
科目： 来源： 题型：
查看答案和解析>>【题目】在如图中，每个正方形由边长为1的小正方形组成：
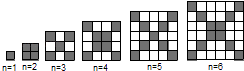
（1）观察图形，请填写下列表格：正方形边长
1
3
5
7
…
n（奇数）
黑色小正方形个数
正方形边长
2
4
6
8
…
n（偶数）
黑色小正方形个数
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1 ， 白色小正方形的个数为P2 ， 问是否存在偶数n，使P2=5P1？若存在，请写出n的值；若不存在，请说明理由．
相关试题
