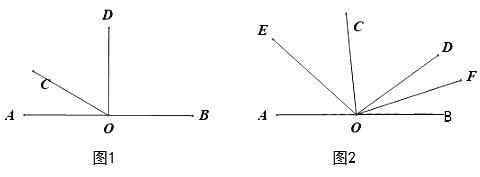
【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
参考答案:
【答案】(1)60°;(2)120°;(3)6秒.
【解析】
(1)根据直角的定义求出∠BOD,再根据3∠AOC=∠BOD可得∠AOC的度数,又因为∠COD与∠AOC 互余即可解答;
(2)不变,是120°.根据(1)求出∠COD的度数,从而求得∠AOC+∠BOD的值, 再利用角平分线定义求出∠EOC +∠DOF,最后根据∠EOF=∠EOC +∠DOF+∠COD即可解答.
(3) 设t秒时,∠COM=∠BON.用含t的式子表示出∠COM、∠BON,从而列出方程求解.
解:(1)因为∠AOD是直角,所以∠AOD= =90°,又因为3∠AOC=∠BOD,所以∠AOC=![]() ∠BOD=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°;
∠BOD=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°;
(2)因为∠AOD是直角,∠AOC=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°,
所以∠AOC+∠BOD=180°-∠COD=180°- 60°=120°,因为OE、OF分别平分∠AOC、∠BOD,所以∠EOC +∠DOF =![]() (∠AOC+∠BOD)=×120°=60°,所以∠EOF=∠EOC +∠DOF+∠COD=60°+60°=120°;
(∠AOC+∠BOD)=×120°=60°,所以∠EOF=∠EOC +∠DOF+∠COD=60°+60°=120°;
(3)设t秒时,∠COM=∠BON.t秒时,∠COM=![]() (180°-∠AOC-20°t)=
(180°-∠AOC-20°t)= ![]() (180°-30°-20°t)=75°-10°t,∠BON=
(180°-30°-20°t)=75°-10°t,∠BON=![]() ∠BOD=
∠BOD=![]() (90°-10°t)=45°-5°t,当∠COM=∠BON时,75°-10°t=45°-5°t,解得:t=6,即6s时,∠COM=∠BON.
(90°-10°t)=45°-5°t,当∠COM=∠BON时,75°-10°t=45°-5°t,解得:t=6,即6s时,∠COM=∠BON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
(1)建立适当的直角坐标系,并写出各个顶点的坐标;
(2)将(1)中各顶点的横坐标都加2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
(3)将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
(4)将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
-
科目: 来源: 题型:
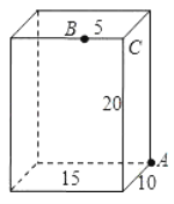
查看答案和解析>>【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。
(1)如图2所示,求
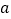 的值;
的值;(2)如图3所示:
①若
 求整式D;
求整式D;②若
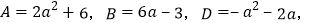 求这九个整式的和是多少。
求这九个整式的和是多少。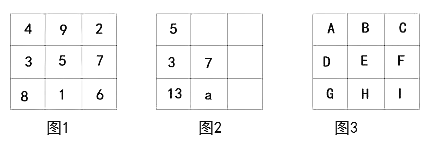
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+2x+2
(1)求该抛物线的对称轴、顶点坐标以及y随x变化情况;
(2)在如图的直角坐标系内画出该抛物线的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列段文字,再解答问题:
已知在平面内有两点
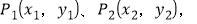 其两点间的距离公式为:
其两点间的距离公式为: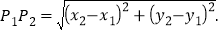
(1)已知点P(2,4)、Q(-3,-8),试求P、Q两点间的距离;
(2)已知点A(0,6)、B(-3,2)、C(3,2),判断线段AB、BC、AC中哪两条线段是相等的?并说明理由;
(3)已知点
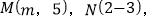 且MN=10,求
且MN=10,求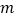 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
相关试题

