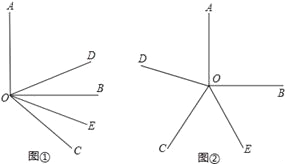
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数;
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,判断∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数.

参考答案:
【答案】(1)∠DOE=45°;(2)∠DOE的大小不变等于45°.理由见解析;(3)∠DOE的大小发生变化,∠DOE=45°或135.
【解析】试题分析:(1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)结合角的特点,∠DOE=∠DOC+∠COE,求得结果进行判断和计算;
(3)正确作出图形,判断大小变化.
试题解析:
解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠COB=35°,∠COD=
∠COB=35°,∠COD=![]() ∠AOC=10°,
∠AOC=10°,
∴∠DOE=45°;
(2)∠DOE的大小不变等于45°.
理由:∠DOE=∠DOC+∠COE=![]() ∠COB+
∠COB+![]() ∠AOC
∠AOC
=![]() (∠COB+∠AOC)
(∠COB+∠AOC)
=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化,∠DOE=45°或135.
如图①,∠DOE=45°;
如图②,∠DOE=135°.(说理过程同(2))
点睛: 此题主要考查了角平分线的性质以及角的有关计算,正确作图,熟记角的特点与角平分线的定义是解决此题的关键.
-
科目: 来源: 题型:
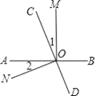
查看答案和解析>>【题目】如图,直线AB,CD相交于O点,OM⊥AB于O.
(1)若∠1=∠2,求∠NOD;
(2)若∠BOC=4∠1,求∠AOC与∠MOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
A.x (x﹣10)=200
B.2x+2 (x﹣10)=200
C.x(x+10)=200
D.2x+2(x+10)=200 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个内角为 50°,则顶角为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用线段垂直平分线性质定理及其逆定理证明以下命题.
已知:如图,AB=AC,DB=DC,点E在AD上.求证:EB=EC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(
 )如图(
)如图( ),
), 是
是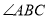 内一定点,
内一定点, 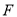 为射线
为射线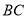 边上一定点,请在射线
边上一定点,请在射线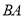 上找一点
上找一点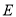 ,使得
,使得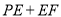 最小.
最小.(
 )如图(
)如图( ),
),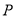 是
是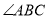 内一定点,点
内一定点,点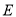 、
、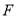 分别为射线
分别为射线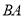 、
、 边上两个动点,请作出使得
边上两个动点,请作出使得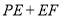 最小的
最小的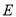 点和
点和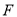 点.
点.(
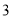 )如图(
)如图(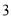 ),
),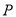 是
是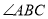 内一定点,点
内一定点,点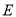 、
、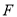 分别为射线
分别为射线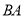 、
、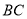 边上两个动点,请作出使得
边上两个动点,请作出使得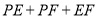 最小的
最小的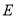 点和
点和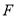 点.
点.拓展应用:
(
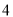 )如图(
)如图( ),
),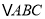 为锐角三角形,
为锐角三角形, 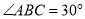 ,
, 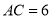 ,
, 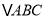 的面积为
的面积为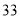 ,点
,点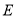 、
、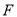 、
、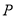 分别为
分别为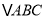 三边
三边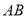 、
、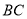 、
、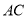 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的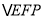 ,并求出
,并求出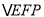 周长的最小值.
周长的最小值.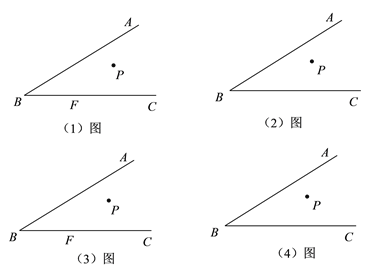
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a是有理数,那么下列各式中一定表示正数的是( )
A. 2018a2 B. a+2018 C. |2018a| D. |a|+2018
相关试题

