【题目】利用线段垂直平分线性质定理及其逆定理证明以下命题.
已知:如图,AB=AC,DB=DC,点E在AD上.求证:EB=EC.

参考答案:
【答案】证明见解析
【解析】试题分析:
由试题中的要求“利用线段垂直平分线性质定理及其逆定理证明以下命题”可知,我们需先证点E在BC的垂直平分线上,所以我们连接BC,由AB=AC,DB=DC可得点A、D均在BC的垂直平分线上,再由“两点确定一条直线”就可得AD是BC的垂直平分线,再由线段垂直平分线的性质就可得到结论.
试题解析:
连结BC.
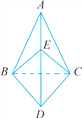
∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵DB=DC,
∴点D在线段BC的垂直平分线上.
∴AD是线段BC的垂直平分线(两点确定一条直线).
又∵点E在AD上,
∴EB=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
A.x (x﹣10)=200
B.2x+2 (x﹣10)=200
C.x(x+10)=200
D.2x+2(x+10)=200 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个内角为 50°,则顶角为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数;
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,判断∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(
 )如图(
)如图(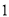 ),
), 是
是 内一定点,
内一定点, 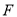 为射线
为射线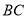 边上一定点,请在射线
边上一定点,请在射线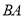 上找一点
上找一点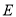 ,使得
,使得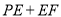 最小.
最小.(
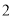 )如图(
)如图( ),
),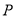 是
是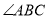 内一定点,点
内一定点,点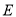 、
、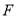 分别为射线
分别为射线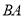 、
、 边上两个动点,请作出使得
边上两个动点,请作出使得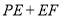 最小的
最小的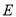 点和
点和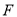 点.
点.(
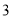 )如图(
)如图(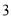 ),
),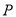 是
是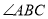 内一定点,点
内一定点,点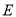 、
、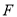 分别为射线
分别为射线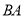 、
、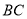 边上两个动点,请作出使得
边上两个动点,请作出使得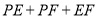 最小的
最小的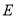 点和
点和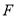 点.
点.拓展应用:
(
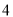 )如图(
)如图( ),
),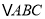 为锐角三角形,
为锐角三角形, 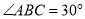 ,
, 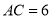 ,
, 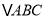 的面积为
的面积为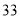 ,点
,点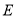 、
、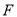 、
、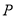 分别为
分别为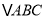 三边
三边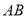 、
、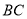 、
、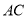 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的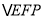 ,并求出
,并求出 周长的最小值.
周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a是有理数,那么下列各式中一定表示正数的是( )
A. 2018a2 B. a+2018 C. |2018a| D. |a|+2018
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的
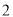 倍,小亮在爸爸出发后
倍,小亮在爸爸出发后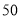 分钟才乘上缆车,缆车的平均速度为
分钟才乘上缆车,缆车的平均速度为 米/分.设爸爸出发
米/分.设爸爸出发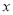 分后行走的路程为
分后行走的路程为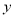 米.图中的折线表示爸爸在整个行走过程中
米.图中的折线表示爸爸在整个行走过程中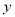 随
随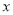 的变化关系.
的变化关系.(
 )爸爸行走的总路程是________米,他途中休息了_________分.
)爸爸行走的总路程是________米,他途中休息了_________分.(
 )请求出爸爸在休息后所走的路程段上的步行速度.
)请求出爸爸在休息后所走的路程段上的步行速度.(
 )当小亮到达缆车终点时,爸爸离缆车终点的路程是多少?
)当小亮到达缆车终点时,爸爸离缆车终点的路程是多少?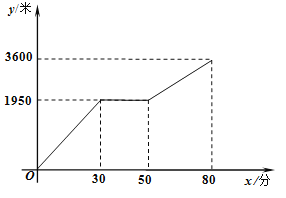
相关试题

