Question

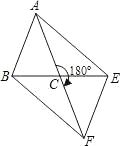
【题目】如图，在△ABC中，AB=AC，若将△ABC绕点C顺时针旋转180°，得到△FEC

（1）猜想AE与BF有何关系，说明理由．

（2）若△ABC的面积为3cm2，求四边形ABFE的面积．

（3）当∠ACB为多少度时，四边形ABFE为矩形？

Answer 1

【答案】（1）AE∥BF，AE=BF（平行四边形的对边平行且相等）；

（2）S四边形ABFE=12cm2；

（3）当∠ACB=60°时，四边形ABFE为矩形．

【解析】

试题分析：（1）由△ABC绕点C顺时针旋转180°可知：AC=CF，BC=CE，四边形ABFE为平行四边形，于是得到结论；

（2）由于AC是△ABE的BE边上中线，于是得到S△ABE=2S△ABC=6，同理S△BEF=2S△CEF=6，即可得到结论；

（3）要判断四边形ABFE为矩形，从对角线来看，要求AF=BE，又AF与BE互相平分，只需要AC=BC，而AB=AC，故△ABC为等边三角形，∠ACB=60°．

试题解析：（1）AE∥BF，AE=BF．

理由是：∵△ABC绕点C顺时针旋转180°得到△FEC，

∴△ABC≌△FEC，

∴AB=FE（全等三角形的对应边相等），

∠ABC=∠FEC（全等三角形的对应角相等），

∴AB∥FE（内错角相等，两直线平行），

∴四边形ABFE为平行四边形（一组对边平行且相等的四边形是平行四边形），

∴AE∥BF，AE=BF（平行四边形的对边平行且相等）；

（2）由（1）得四边形ABFE为平行四边形，

∴AC=CF，BC=CE，

∴根据等底同高得到S△ABC=S△ACE=S△BCF=S△CEF=3，

S四边形ABFE=4S△ABC=12cm2；

（3）当∠ACB=60°时，四边形ABFE为矩形．

理由是：AB=AC，∠ACB=60°，

∴△ABC是等边三角形，

∴BC=AC，∠BAC=60°，

∴∠ACE=120°．

又BC=CE，AC=CF，

∴∠EAC=∠CEA=30°，

∴∠BAE=90°，同理可证其余三个角也为直角．

∴四边形ABFE为矩形．