【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
参考答案:
【答案】(1)见解析(2)![]()
【解析】
试题(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
试题解析:(1)证明:在ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=![]() AD.
AD.
又∵CE=![]() BC,
BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
如图,过点D作DH⊥BE于点H.
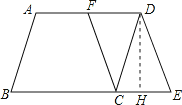
在ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=![]() CD=2,DH=2
CD=2,DH=2![]() .
.
在CEDF中,CE=DF=![]() AD=3,则EH=1.
AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE=![]() .
.
-
科目: 来源: 题型:
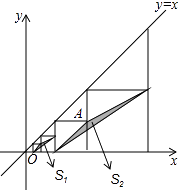
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则Sn的值为 . (用含n的代数式表示,n为正整数)
-
科目: 来源: 题型:
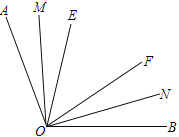
查看答案和解析>>【题目】如图,线段OA绕点O逆时针旋转一周,满足∠EOF始终在∠AOB的内部且∠EOF=58°.线段OM、ON分别为∠AOE和∠BOF的平分线,在旋转过程中,∠MON的最大值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
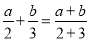 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: 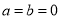 .我们称使得
.我们称使得 成立的一对数
成立的一对数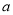 ,
, 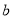 为“相伴数对”,记为
为“相伴数对”,记为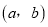 .
.(1)若
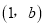 是“相伴数对”,求
是“相伴数对”,求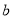 的值;
的值;(2)写出一个“相伴数对”
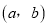 ,其中
,其中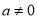 且
且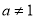 ;
;(3)若
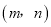 是“相伴数对”,求代数式
是“相伴数对”,求代数式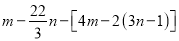 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=


(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)所作的圆中,圆心角∠BOC=°,圆的半径为 , 劣弧 的长为 .
的长为 . -
科目: 来源: 题型:
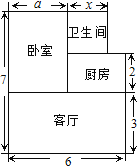
查看答案和解析>>【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算
 的面积;
的面积;方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段AB=4(单位长度),CD=6(单位长度),点A在数轴上表示的数是-16,点C在数轴上表示的数是18

(1) 点B在数轴上表示的数是多少,点D在数轴上表示的数是多少,线段AD等于 多少;
(2) 若线段AB以4个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动,设运动时间为t秒
①若BC=6(单位长度),求t的值
②当0<t<5时,设M为AC中点,N为BD中点,求线段MN的长
相关试题

