【题目】如图,数轴上线段AB=4(单位长度),CD=6(单位长度),点A在数轴上表示的数是-16,点C在数轴上表示的数是18
![]()
(1) 点B在数轴上表示的数是多少,点D在数轴上表示的数是多少,线段AD等于 多少;
(2) 若线段AB以4个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动,设运动时间为t秒
①若BC=6(单位长度),求t的值
②当0<t<5时,设M为AC中点,N为BD中点,求线段MN的长
参考答案:
【答案】(1)-12, 24, 40; (2) ①点B,C相遇之前,t=4, 点B,C相遇之后,t=6, ② MN=5.
【解析】
(1)由线段AB=4,点A在数轴上表示的数是-16,根据两点间的距离公式可得点B在数轴上表示的数是-16+4=-12.由CD=6,点C在数轴上表示的数是18,根据两点间的距离公式可得点D在数轴上表示的数是18+6=24,根据两点间的距离公式可得AD=24-(-16)=40;
(2)①设运动t秒时,BC=6(单位长度),然后分点B在点C的左边和右边两种情况,根据题意列出方程求解即可;
②当0<t<5时,B与C没有相遇,分别求出此时A,B,C,D四点表示的数,再根据中点坐标公式求出M,N表示的数,然后利用两点间的距离公式即可求出线段MN的长.
解:(1)∵线段AB=4,点A在数轴上表示的数是-16,
∴点B在数轴上表示的数是-16+4=-12.
∵CD=6,点C在数轴上表示的数是18,
∴点D在数轴上表示的数是18+6=24,
∴AD=24-(-16)=40.
故答案为-12,24,40;
(2)①设运动t秒时,BC=6单位长度,
Ⅰ)当点B在点C的左边时,
由题意得:4t+6+2t=30,
解得:t=4;
Ⅱ)当点B在点C的右边时,
由题意得:4t-6+2t=30,
解得:t=6.
综上可知,若BC=6(单位长度),t的值为4或6秒;
②当0<t<5时,
A点表示的数为-16+4t,B点表示的数为-12+4t,
C点表示的数为18-2t,D点表示的数为24-2t,
∵M为AC中点,N为BD中点,
∴M(1+t),N(6+t)
∴MN=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连结DE,CF。
BC,连结DE,CF。
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=


(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)所作的圆中,圆心角∠BOC=°,圆的半径为 , 劣弧 的长为 .
的长为 . -
科目: 来源: 题型:
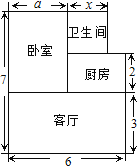
查看答案和解析>>【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算
 的面积;
的面积;方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.
(1)求中巴车和大客车各有多少个座位?
(2)客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 :
: 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 :
: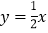 交于点A.
交于点A. 分别求出点A、B、C的坐标;
分别求出点A、B、C的坐标; 直接写出关于x的不等式
直接写出关于x的不等式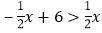 的解集;
的解集; 若D是线段OA上的点,且
若D是线段OA上的点,且 的面积为12,求直线CD的函数表达式.
的面积为12,求直线CD的函数表达式.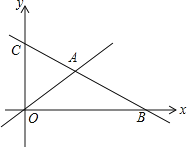
-
科目: 来源: 题型:
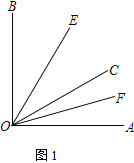
查看答案和解析>>【题目】已知∠AOB内部有3条射线OE、OC、OF
(1) 如图1,若∠AOB = 90°,∠AOC = 30°,OE平分∠BOC,OF平分∠AOC,求∠EOF的度数.
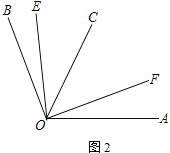
(2) 如图2,若∠AOB = α,∠EOB = ∠COB,∠COF = ∠FOA,求∠EOF的度数(用含α的式子表示)
相关试题

