【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一: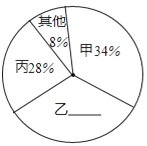
图一
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示: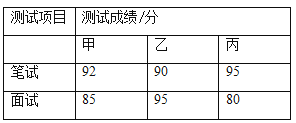
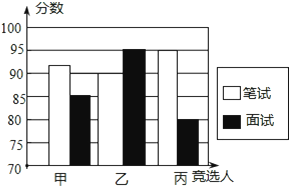
图二是某同学根据上表绘制的一个不完全的条形图.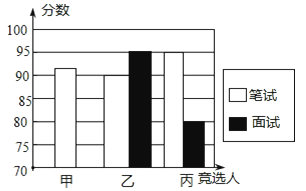
图二
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
参考答案:
【答案】
(1)
解答:解:
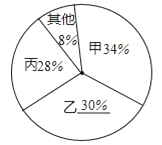
图一 图二
(2)
解答:根据题意得:甲的票数是:200×34%=68(票),乙的票数是:200×30%=60(票),丙的票数是:200×28%=56(票).
所以甲的票数是68票,乙的票数是60票,丙的票数是56票.
(3)
解答:应该录取丙.根据题意得:甲的平均成绩: ![]() ,乙的平均成绩:
,乙的平均成绩: ![]() ,丙的平均成绩:
,丙的平均成绩: ![]() ,∵丙的平均成绩最高,∴应该录取丙.
,∵丙的平均成绩最高,∴应该录取丙.
【解析】(1)由图1可看出,乙的得票所占的百分比为1减去“丙+甲+其他”的百分比;(2)由题意可分别求得三人的得票数,甲的得票数200×34%,乙的得票数200×30%,丙的得票数200×28%;(3)由题意可分别求得三人的得分,比较得出结论.
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x+3)2=16可转化为两个一元一次方程,其中一个一元次方程是x+3=4,则另一个一元一次方程是( )
A.x-3=-4B.x-3=4C.x+3=4D.x+3=-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×4的正方形网格中,点A、B、C、D、E、F都在格点上.连接点A、B得线段AB.
(1)连接C、D、E、F中的任意两点,共可得 条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是 ;
(3)用三角尺或量角器度量、检验,AB及(1)中所连得的线段中,互相垂直的线段有几对?(请用“⊥”表示出来) .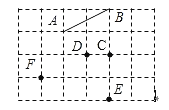
-
科目: 来源: 题型:
查看答案和解析>>【题目】某广告公司欲招聘策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项成绩如下表所示:

(1)若根据三次测试的平均成绩确定录取人选,那么谁被录取?说明理由.
(2)若公司将创新能力、综合知识、计算机各项得分按4:3:1的比例确定各人的成绩,此时谁被录取?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】要使(x2+ax+1)(﹣6x3)的展开式中不含x4项,则a= _________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位面向内部职工招聘高级管理人员一名.经初选、复选后,共有甲、乙、丙三名候选人进入最后的决赛.现对甲、乙、丙三人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
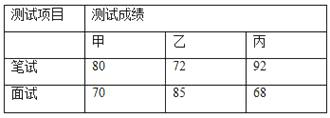
除了笔试、面试外,根据录用程序,该单位还组织了200名职工利用投票推荐的方式对三人进行民主评议,三人的得票率如下图所示(没有弃权票,每位职工只能推荐1人),每得一票记1分.
(1)甲的民主评议得分为多少?
(2)若根据笔试成绩、面试成绩、民主评议得分三项的平均成绩确定个人成绩,那么谁将被录用?
(3)根据实际需要,该单位将笔试、面试、民主评议三项得分按5:3:2的比例确定个人成绩,那么谁将被录用?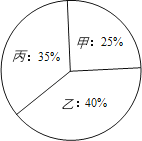
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式ax2+2a2x+a3分解因式的结果是 .
相关试题

