【题目】水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何随着时间t变化的,请选择匹配的示意图与容器.
(A)——( ) (B)——( )
(C)——( ) (D)——( )

参考答案:
【答案】(A)——(3),(B)——(2),(C)——(4) , (D)——(1)
【解析】
根据各图中水高度与时间的关系进行判断即可.
A、B的直径上下一致,所以水的高度和时间之间对应的示意图为(2)、(3),由于A的直径小,B的直径大,A中水面上升的速度大于B,所以A对应(3),B对应(2),C为下大上小的锥形,随着水面的升高,横截面积越来越小,水面上升的速度会越来越快,故选(4),D的下部为圆球型,上部为圆柱形,随着水面的升高,横截面积越来越大,水面上升的速度会越来越慢,当达到球体的一半时,水面上升的速度会越来越快,所以水的高度和时间之间对应的示意图是(1).
故答案为:(A)——(3),(B)——(2),(C)——(4) , (D)——(1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE______DB(填“>”,“<”或“=”).
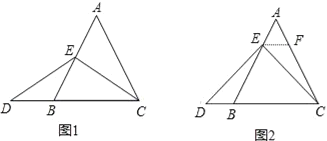
(2)一般情况,证明结论:
如图2,过点E作EF∥BC,交AC于点F.(请你继续完成对以上问题(1)中所填写结论的证明)
(3)拓展结论,设计新题:
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC. 若△ABC的边长为1,AE=2,则CD的长为_______(请直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
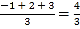 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;

(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;

(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
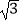 ﹣2)0+(
﹣2)0+(  )﹣1+4cos30°﹣|
)﹣1+4cos30°﹣| 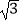 ﹣
﹣  |
|
相关试题

