【题目】数学课上,李老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE______DB(填“>”,“<”或“=”).
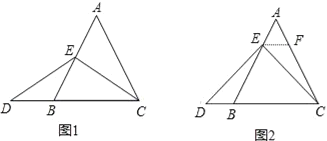
(2)一般情况,证明结论:
如图2,过点E作EF∥BC,交AC于点F.(请你继续完成对以上问题(1)中所填写结论的证明)
(3)拓展结论,设计新题:
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC. 若△ABC的边长为1,AE=2,则CD的长为_______(请直接写出结果).
参考答案:
【答案】(1)=;(2)=;(3)1或3.
【解析】
(1)当E为中点时,过E作EF∥BC交AC于点F,则可证明△BDE≌△FEC,可得到AE=DB;
(2)类似(1)过E作EF∥BC交AC于点F,可利用AAS证明△BDE≌△FEC,可得BD=EF,再证明△AEF是等边三角形,可得到AE=EF,可得AE=DB;
(3)分为四种情况:画出图形,根据等边三角形性质求出符合条件的CD即可.
解:(1)如图1,过点E作EF∥BC,交AC于点F,

∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,

∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
故答案为:=;
(2)如图2,过点E作EF∥BC,交AC于点F,
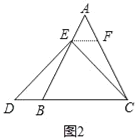
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中

∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD.
(3)解:分为四种情况:
如图3,
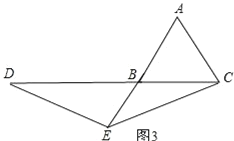
∵AB=AC=1,AE=2,
∴B是AE的中点,
∵△ABC是等边三角形,
∴AB=AC=BC=1,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°﹣30°﹣60°=90°,
即△DEB是直角三角形.
∴BD=2BE=2(30°所对的直角边等于斜边的一半),
即CD=1+2=3.
如图4,
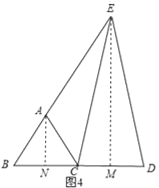
过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,EC=ED,
∴BN=CN=![]() BC=
BC=![]() ,CM=MD=
,CM=MD=![]() CD,AN∥EM,
CD,AN∥EM,
∴△BAN∽△BEM,
∴![]() ,
,
∵△ABC边长是1,AE=2,
∴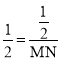 ,
,
∴MN=1,
∴CM=MN﹣CN=1﹣![]() =
=![]() ,
,
∴CD=2CM=1;
如图5,

∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
如图6,
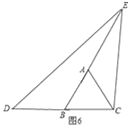
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
答:CD的长是3或1.
故答案为:1或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由.
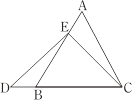
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何随着时间t变化的,请选择匹配的示意图与容器.
(A)——( ) (B)——( )
(C)——( ) (D)——( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
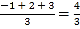 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;

(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;

(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.

相关试题

