搜索
【题目】如图，已知ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC+BD=24厘米，△OAB的周长是18厘米，则EF的长是（ ）厘米．
A．6 B．9 C．12 D．3
参考答案：
【答案】D
【解析】
试题分析：根据平行四边形的性质可知OA=
AC，OB=BD，结合AC+BD=24厘米，△OAB的周长是18厘米，求出AB的长，利用三角形中位线定理求出EF的长．
解：∵ABCD的对角线AC，BD相交于点O，
∴OA=OC，OB=OD，
∵AC+BD=24厘米，
∴OB+0A=12厘米，
∵△OAB的周长是18厘米，
∴AB=18﹣12=6厘米，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=AB=3厘米，
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若点A（a+1，b﹣2）在第二象限，则点B（﹣a，b+1）在（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是( )
A. 各边都相等的多边形叫正多边形 B. 圆上任意两点间的距离叫弧
C. 三角形是多边形 D. 八边形有八个顶点，八个内角，八条对角线
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班数学兴趣小组进行了如下探究：（1）如图①，若四边形ABCD是矩形，对角线AC、BD交点为P，过点P作PQ⊥BC于点Q，连结DQ交AC于点P1，过点P1作P1Q1⊥BC于点Q1，已知AB=CD=a，则PQ= ，P1Q1= ．（用含a的代数式表示）
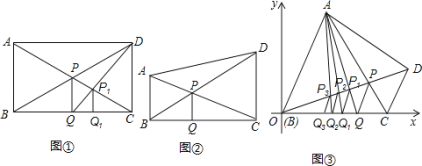
（2）如图②，在直角梯形ABCD中，AB∥CD，∠ABC=90°，AC、BD交于点P，过点P作PQ⊥BC于点Q．已知AB=a，CD=b，请用含a、b的代数式表示线段PQ的长，写出你的解题过程．
（3）如图③，在直角坐标系xOy中，梯形ABCD的腰BC在x轴正半轴上（点B与原点O重合），AB∥CD，∠ABC=60°，AC、BD交于点P，过点P作PQ∥CD交BC于点Q，连结AQ交BD于点P1，过点P1作P1Q1∥CD交BC于点Q1．连结AQ1交BD于点P2，过点P2作P2Q2∥CD交BC于点Q2，…，已知AB=a，CD=b，则点P1的纵坐标为 点Pn的纵坐标为 （直接用含a、b、n的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】扬州市中小学全面开展“体艺2+1”活动，某校根据学校实际，决定开设A：篮球，B：乒乓球，C：声乐，D：健美操等四中活动项目，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制了两幅不完整的统计图．请回答下列问题：
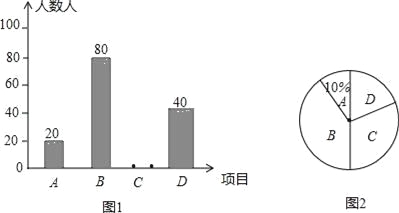
（1）这次被调查的学生共有 人．
（2）请你将统计图1补充完整．
（3）统计图2中D项目对应的扇形的圆心角是 度．
（4）已知该校学生2400人，请根据调查结果估计该校最喜欢乒乓球的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若3a﹣2b=2，则代数式1﹣6a+4b=______;
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b；如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（ ）
A．0 B．2 C．3 D．4
相关试题
