【题目】请阅读如下材料.
如图,已知正方形ABCD的对角线AC、BD于点O,E是AC上一点,AG⊥BE,垂足为G.求证:OE=OF.
证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,且OA=OE.
又∵AG⊥BE,∴∠1+∠3=90°=∠2+∠3,即∠1=∠2.
∴Rt△BOE≌Rt△AOF,∴OE=OF.

⑴根据你的理解,上述证明思路的核心是利用 使问题得以解决,而证明过程中的关键是证出 .
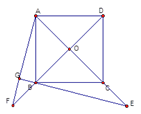
⑵若上述命题改为:点E在AC的延长线上,AG⊥BE交EB的延长线于点G,延长AG交DB的延长线于点F,如图,其他条件不变.
求证:OF=OE.
参考答案:
【答案】⑴三角形全等,∠1=∠2;(2)见解析;
【解析】试题分析:(1)根据正方形的对角线相等且、互相垂直平分证明出∠1=∠2;再根据AAS证明出Rt△BOE≌Rt△AOF,根据全等三全等的性质即可证明OE=OF;
(2)根据正方形的四边相等,每条对角线平分一组对角,证明出∠ABF=∠BCE,从而证明出△ABF≌△BCE,根据全等三全等的性质即可证明OE=OF.
试题解析:(1)上述证明思路的核心是利用全等三角形的性质使问题得以解决,而证明过程中的关键是证出∠1=∠2;
故答案为:全等三角形的性质使问题得以解决;∠1=∠2.
(2)∵ABCD是正方形,
∴∠ABO=∠ACB=45° ,AB=BC, OB=OC,
∴∠ABF=∠BCE=135° ,
∵∠OAF+∠F=90° ,∠OAF+∠E=90°,
∴△ABF≌△BCE(AAS)
∴BF=CE,
∴BF+OB=CE+OC,即OE=OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,计算正确的是( )
A.(a2b)3=a5b3
B.(3a2)3=27a6
C.x6÷x2=x3
D.(a+b)2=a2+b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】李红同学为了在中考体育加试中取得好成绩,每天自己在家里练习做一分钟仰卧起坐,妈妈统计了她一个星期做的次数:30、28、24、30、25、30、22.则李红同学一个星期做仰卧起坐的次数的中位数和众数分别是_______▲____
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则它最后的单价是( )元.
A. aB. 0.99aC. 1.21aD. 0.81a
-
科目: 来源: 题型:
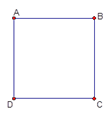
查看答案和解析>>【题目】如图,四边形ABCD是一个正方形.
⑴请你在平面内找到一个点O,并连接OA、OB、OC、OD使得到△OAB、△BOC、△COD、△OAD都是等腰三角形.
⑵这样的点,你能找到多少个?
⑶试写出你找到的等腰三角形的顶角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖场2013年底的生猪出栏价格是每千克a元,受市场影响,2014年第一季度出栏价格平均每千克下降了15%,到了第二季度平均每千克比第一季度又上升了20%,则第三季度初这家养殖场的生猪出栏价格是每千克( )
A. (1﹣15%)(1+20%)a元B. (1﹣15%)20%a元
C. (1+15%)(1﹣20%)a元D. (1+20%)15%a元
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一句地方民谣“早穿皮袄午穿纱”,说明此地气温的特点的特征数是( )
A. 平均数 B. 中位数 C. 极差 D. 众数
相关试题

