【题目】如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：
①OA=OD；
②AD⊥EF；
③AE+DF=AF+DE；
④当∠BAC=90°时，四边形AEDF是正方形．
其中一定正确的是（ ）

A.①②③
B.②③④
C.①③④
D.①②③④

参考答案：

【答案】B
【解析】解：如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，

∴①不正确；

∵AD是△ABC的角平分线，

∴∠EAD∠FAD，

在△AED和△AFD中，

，

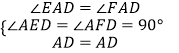∴△AED≌△AFD（AAS），

∴AE=AF，DE=DF，

∴AE+DF=AF+DE，

∴③正确；

在△AEO和△AFO中，

，

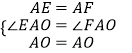∴△AE0≌△AF0（SAS），

∴EO=FO，

又∵AE=AF，

∴AO是EF的中垂线，

∴AD⊥EF，

∴②正确；

∵当∠A=90°时，四边形AEDF的四个角都是直角，

∴四边形AEDF是矩形，

又∵DE=DF，

∴四边形AEDF是正方形，

∴④正确．

综上，可得正确的是：②③④．

所以答案是：B．

【考点精析】掌握线段垂直平分线的判定和角的平分线判定是解答本题的根本，需要知道和一条线段两个端点距离相等的点，在这条线段的垂直平分线上；可以证明三角形内存在一个点，它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)．

关闭