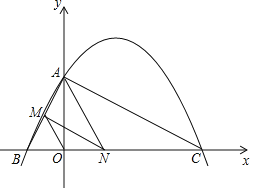
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)N(3,0);(3)OM=
x+4;(2)N(3,0);(3)OM=![]() AC.
AC.
【解析】
试题分析:(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=![]() AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
试题解析:(1)将点B,点C的坐标分别代入y=ax2+bx+4可得
![]() ,
,
解得 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),
则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]() ,
,
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM=![]() AB,
AB,
∵AB=![]() ,AC=
,AC=![]() ,
,
∴AB=![]() AC,
AC,
∴OM=![]() AC.
AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是方程x2-a=0的解,则a=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E,且DE=4,则AD+AE的长度为________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是真命题的是( )
A. 对顶角相等 B. 如果两个角是直角那么这两个角相等
C. 全等三角形的对应角等 D. 两直线平行,内错角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,以下作图不可能的是( )
A. 在AB上取一点C,使AC=BC
B. 在AB的延长线上取一点C,使BC=AB
C. 在BA的延长线上取一点C,使BC=AB
D. 在BA的延长线上取一点C,使BC=2AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面内任意一个四边形ABCD,现从以下四个关系式①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C 中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的组合是 .
相关试题

