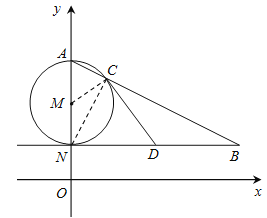
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

参考答案:
【答案】(1) B(![]() ,2).(2)证明见解析.
,2).(2)证明见解析.
【解析】
试题分析:(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
试题解析:(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=![]() ,
,
∴B(![]() ,2).
,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=![]() NB=ND,
NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,如果有一个角等于40°,那么另两个角等于______________ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠1=70°,则∠BAC的大小为( )
A.30°
B.40°
C.50°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是方程x2-a=0的解,则a=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E,且DE=4,则AD+AE的长度为________________
-
科目: 来源: 题型:
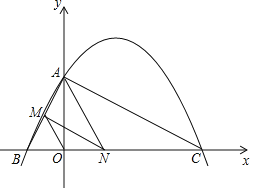
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是真命题的是( )
A. 对顶角相等 B. 如果两个角是直角那么这两个角相等
C. 全等三角形的对应角等 D. 两直线平行,内错角相等
相关试题

