【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
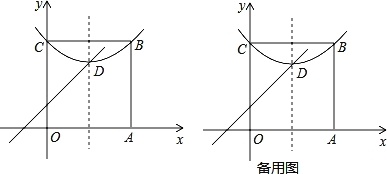
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
参考答案:
【答案】(1)、x=m,y=n,y=x+n﹣m,y=﹣x+m+n;(2)、y=![]() (x﹣2)2+3;(3)、
(x﹣2)2+3;(3)、![]() 或
或![]()
【解析】
试题分析:(1)、根据特征线直接求出点D的特征线;(2)、由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;(3)、分平行于x轴和y轴两种情况,由折叠的性质计算即可.
试题解析:(1)、∵点D(m,n), ∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n;
(2)、点D有一条特征线是y=x+1, ∴n﹣m=1, ∴n=m+1
∵抛物线解析式为![]() , ∴y=
, ∴y=![]() (x﹣m)2+m+1,
(x﹣m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n), ∴B(2m,2m),
∴![]() (2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=
(2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=![]() (x﹣2)2+3
(x﹣2)2+3
(3)、如图,当点A′在平行于y轴的D点的特征线时,
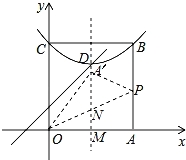
根据题意可得,D(2,3), ∴OA′=OA=4,OM=2, ∴∠A′OM=60°, ∴∠A′OP=∠AOP=30°,
∴MN=![]() =
=![]() , ∴抛物线需要向下平移的距离=3﹣
, ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() .
.
当点A′在平行于x轴的D点的特征线时,
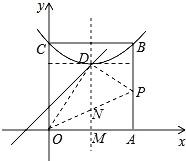
∵顶点落在OP上, ∴A′与D重合, ∴A′(2,3), 设P(4,c)(c>0),
由折叠有,PD=PA, ∴![]() =c, ∴c=
=c, ∴c=![]() , ∴P(4,
, ∴P(4,![]() ) ∴直线OP解析式为y=
) ∴直线OP解析式为y=![]() ,
,
∴N(2,![]() ), ∴抛物线需要向下平移的距离=3﹣
), ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() ,
,
抛物线向下平移![]() 或
或![]() 距离,其顶点落在OP上.
距离,其顶点落在OP上.
考点(1)、折叠的性质;(2)、正方形的性质;(3)、特征线的理解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )
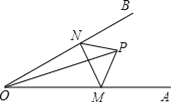
A. 25° B. 30° C. 35° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】解一元二次方程:x2﹣x﹣6=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述正确的是( )
A.任意两个正方形一定是相似的
B.任意两个矩形一定是相似的
C.任意两个菱形一定是相似的
D.任意两个等腰梯形一定是相似的 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山西省第19题)请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德(Archimedes,公元前287~公元212年,古希腊)是有史以来最伟大的数学家之一.他与牛顿、高斯并称为三大数学王子.
阿拉伯Al-Biruni(973年~1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》,第一题就是阿基米德的折弦定理.
阿基米德折弦定理:如图1,AB和BC是
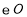 的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是
的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是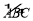 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.∵M是
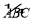 的中点, ∴MA=MC ...
的中点, ∴MA=MC ...
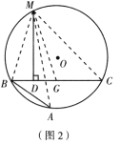
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图(3),已知等边△ABC内接于
 ,AB=2,D为
,AB=2,D为 上一点,
上一点, 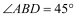 ,AE⊥BD与点E,则△BDC的长是 .
,AE⊥BD与点E,则△BDC的长是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】56°24′=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个三角形相似,如果其中一个三角形的两个内角分别是45°、60°,那么另外一个三角形的最大内角是_____°.
相关试题

