【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 ![]() 交AB于点E,以点B为圆心,BC的长为半径作
交AB于点E,以点B为圆心,BC的长为半径作 ![]() 交AB于点D,则阴影部分的面积为 .
交AB于点D,则阴影部分的面积为 . 
参考答案:
【答案】π﹣2
【解析】解:∵∠ACB=90°,AC=BC=2, ∴S△ABC= ![]() ×2×2=2,
×2×2=2,
S扇形BCD= ![]() =
= ![]() π,
π,
S空白=2×(2﹣ ![]() π)=4﹣π,
π)=4﹣π,
S阴影=S△ABC﹣S空白=2﹣4+π=π﹣2,
所以答案是π﹣2.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
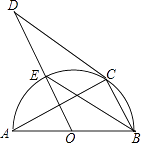
A.AC⊥BC
B.BE平分∠ABC
C.BE∥CD
D.∠D=∠A -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为 .
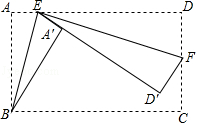
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个标志中,是轴对称图形的是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
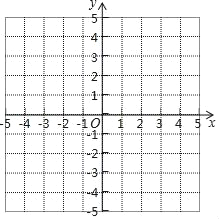
查看答案和解析>>【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(2,4)、B(﹣3,﹣2)、C(3,1).
(1)请在这个坐标系中作出△ABC和关于y轴对称的△A1B1C1.
(2)分别写出点A1、B1、C1的坐标.
相关试题

