【题目】观察下列三行数:

(1)第①行的第n个数是_______(直接写出答案,n为正整数)
(2)第②、③行的数与第①行相对应的数分别有什么关系?
(3)取每行的第9个数,记这三个数的和为a,化简计算求值:(5a2-13a-1)-4(4-3a+![]() a2)
a2)
参考答案:
【答案】(1)-(-2)n;(2)第②行数等于第①行数相应的数减去2;第③行数等于第①行数相应的数除以(-2);(3)-783
【解析】
第一个有符号交替变化的情况时,可以考虑在你所找到的规律代数式中合理的加上负号,并检验计算结果。
(1)首先2 4 8 16 很显然后者比前者多一个二倍。那么通项(一串数列具有代表性的代数式)中绝对含有![]() ,前面加上负号。考虑到数值的变化可以用
,前面加上负号。考虑到数值的变化可以用![]() 表示。
表示。
(2)第②行数等于第①行数相应的数减去2
第③行数等于第①行数相应的数除以(-2)
(3)原式=![]()
第①行的第9个数为512,第②行的第9个数为510,第③行的第9个数为-256,所以
![]() ,将a的值代入上式,得原式=-783.
,将a的值代入上式,得原式=-783.
-
科目: 来源: 题型:
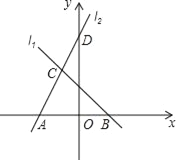
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江夏区某出租车在某一天以江夏体育馆为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9,-2,-5,-4,-12,+8,+3,-1,-4,+10
(1)将最后一名乘客送到目的地,出租车离江夏体育馆出发点多远?
(2)直接写出该出租车在行驶过程中,离江夏体育馆最远的距离是______.
(3)出租车按物价部门规定,行程不超过3km的(含3km),按起步价8元收费,若行程超过3km的,则超过的部分,每千米加收1.2元,该司机这天的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:M=3a2+4ab -5a-6,N=a2-2ab-4
(1)化简:5M-(3N + 4M),结果用含a、b的式子表示.
(2)若式子5M-(3N + 4M)的值与字母a的取值无关,求b4+
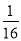 M-
M-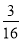 N-
N- 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
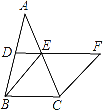
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
相关试题

