【题目】如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是cm. 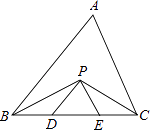
参考答案:
【答案】5
【解析】解:∵BP、CP分别是∠ABC和∠ACB的角平分线, ∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm.
故答案为:5.
分别利用角平分线的性质和平行线的判定,求得△DBP和△ECP为等腰三角形,由等腰三角形的性质得BD=PD,CE=PE,那么△PDE的周长就转化为BC边的长,即为5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件产品原来每件的成本是1000元,由于连续两次降低成本,现在的成本是810元,则平均每次降低成本( )
A. 8.5%B. 9%C. 9.5%D. 10%
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年一季度,某省的进出口总额为214.7亿元,数据“214.7亿”用科学记数法表示为( )
A. 2.147×102B. 2.147×1010C. 0.2147×103D. 0.2147×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,已知AB=CD,若再增加一个_________条件(只填写一个)可得四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出;怎样计算1×2+2×3+3×4+…+(n﹣1)×n呢?
材料学习
计算1+2+3…+n
因为1= (1×2﹣0×1);2=
(1×2﹣0×1);2=  (2×3﹣1×2);3=
(2×3﹣1×2);3=  (3×4﹣2×3)
(3×4﹣2×3)
…,n= [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
所以1+2+3+…+n
= (1×2﹣0×1)+
(1×2﹣0×1)+  (2×3﹣1×2)+
(2×3﹣1×2)+  (3×4﹣2×3)+…+
(3×4﹣2×3)+…+  [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
= [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=
[1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=  n(n+1)
n(n+1)
(1)探究应用
观察规律:①1×2= (1×2×3﹣0×12);②2×3=
(1×2×3﹣0×12);②2×3=  (2×3×4﹣1×2×3);
(2×3×4﹣1×2×3);
③3×4= (3×4×5﹣2×3×4);…
(3×4×5﹣2×3×4);…
猜想归纳:
根据(1)中观察的规律直接写出:4×5= ()
()
(n﹣1)×n= []
[]
问题解决:
1×2+2×3+3×4+4×5…+(n﹣1)×n
= (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+  (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+  (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+  []
[]
=
(2)拓展延伸
根据上面的规律,请直接写出1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n= . -
科目: 来源: 题型:
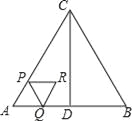
查看答案和解析>>【题目】如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD﹣DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
(1)当点Q在线段AD上时,用含t的代数式表示QR的长;
(2)求点R运动的路程长;
(3)当点Q在线段AD上时,求S与t之间的函数关系式;
(4)直接写出以点B、Q、R为顶点的三角形是直角三角形时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD//BC,AD=BC,则四边形ABCD是_______四边形.
相关试题

