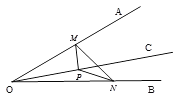
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
A. 2 B. 4 C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,则此时M、N符合题意,求出线段P1P2的长即可.
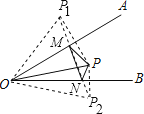
解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,
与OA的交点即为点M,与OB的交点即为点N,此时△PMN的最小周长
∵点P关于OA的对称点为P1,关于OB的对称点为P2,连结OP1、OP2,
∴PM= P1M,OP=O P1,∠P1OA=∠POA;
∵点P关于OB的对称点为P2,
∴PN= P2N,OP=O P2,∠P2OB=∠POB,
∴OP1=OP2=OP=4,
∠P1OP2=∠P1OA+∠POA+∠POB+∠P2OB=2∠POA+2∠POB=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴P1P2=OP1=4,
∴△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2=4
即△PMN的周长的最小值是4.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.65
1.4
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n(n═1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
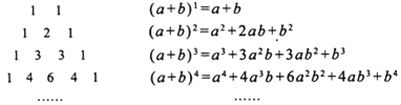
请依据上述规律,写出(x﹣2)2018展开式中含x2017项的系数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(数学阅读)
如图1,在△ABC中,AB=AC,点P为边BC上的任意一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
小尧的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
(推广延伸)
如图3,当点P在BC延长线上时,其余条件不变,请运用上述解答中所积累的经验和方法,猜想PD,PE与CF的数量关系,并证明.
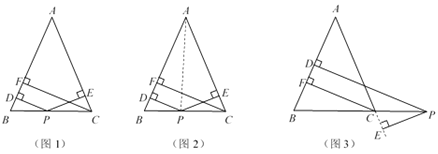
(解决问题)
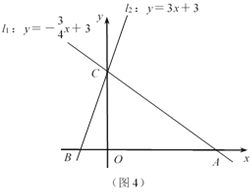
如图4,在平面直角坐标系中有两条直线l1:y=-
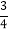 x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.(1)两条直线的交点C的坐标为 ;
(2)说明△ABC是等腰三角形;
(3)若l2上的一点M到l1的距离是1,运用上面的结论,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)3x3x9﹣2xx3x8
(2)﹣12+20160+(
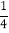 )2017×(﹣4)2018
)2017×(﹣4)2018(3)(x+4)(x﹣4)﹣(x﹣2)2
(4)ab(a+b)﹣(a﹣b)(a2+b2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
①(x﹣1)(x+1)=x2﹣1
②(x﹣1)(x2+x+1)=x3﹣1
③(x﹣1)(x3+x2+x+1)=x4﹣1
……
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1
(2)若x3+x2+x+1=0,求x2019的值
相关试题

