【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P点对应的数:__________;
用含t的代数式表示点P和点C的距离:PC=_____________.
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,
①点P、Q同时运动运动的过程中有__________处相遇,相遇时t=_______________秒.
②在点Q开始运动后,请用t的代数式表示P、Q两点间的距离.(友情提醒:注意考虑P、Q的位置)
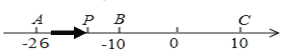
参考答案:
【答案】(1)-26+t;36-t;
(2)2处,24秒和30秒;
(3)当16≤t≤24时 PQ=﹣2t+48;
当24<t≤28时 PQ=2t-48;
当28<t≤30时 PQ= 120﹣4t;
当30<t≤36时 PQ= 4t﹣120
【解析】(1)根据两点间的距离,可得P到点A和点C的距离;
(2)根据两点间的距离,要对t分类讨论,t不同范围,可得不同PQ.
解:(1)P点对应的数为﹣26+t;PC=36﹣t;
故答案为:﹣26+t;36﹣t;
(2)①有2处相遇,
分两种情况:
Q返回前相遇:3(t﹣16)=t,
解得:t=24,
Q返回后相遇:3(t﹣16)+t=36×2,
解得:t=30.
综上所述,相遇时t=24秒或30秒.
故答案为: 24或30;
②当16≤t≤24时,PQ=t﹣3(t﹣16)=﹣2t+48;
当24<t≤28时,PQ=3(t﹣16)﹣t=2t﹣48;
当28<t≤30时,PQ=72﹣3(t﹣16)﹣t=120﹣4t;
当30<t≤36时,PQ=t﹣[72﹣3(t﹣16)]=4t﹣120;
当36<t≤40时,PQ=3(t﹣16)﹣36=3t-84.
“点睛”本题考查了数轴,一元一次方程的应用,解答(2)②题要对t分类讨论是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
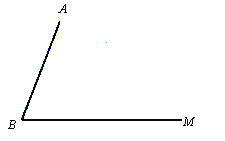
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
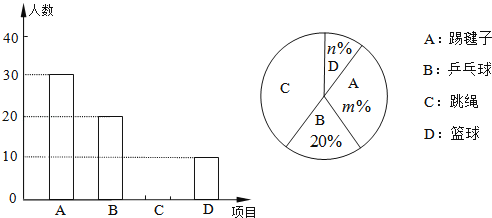
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段文字:
问题:0.
 能用分数表示吗?
能用分数表示吗?探求:步骤①设x=0.
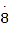 ,
,步骤②10x=10×0.
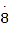 ,
,步骤③10x=8.
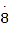 ,
,步骤④10x=8+0.
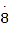 ,
,步骤⑤10x=8+x,
步骤⑥9x=8,
步骤⑦x=
 .
.根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是______;
(2)仿照上述探求过程,请你尝试把0.
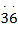 表示成分数的形式.
表示成分数的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若A﹣B=1,则称A与B是关于1的单位数.
(1)3与______是关于1的单位数,x﹣3与______是关于1的单位数.(填一个含x的式子)
(2)若A=3x(x+2)﹣1,
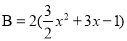 ,判断A与B是否是关于1的单位数,并说明理由.
,判断A与B是否是关于1的单位数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】 请阅读下列材料,并解答相应的问题:
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”中国古代称“幻方”为“河图“、“洛书“等,例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
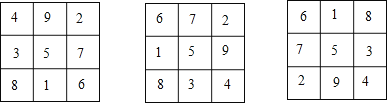
(1)设图1的三阶幻方中间的数字是x,用x的代数式表示幻方中9个数的和为 ;
(2)请你将下列九个数:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分别填入图2方格中,使得每行、每列、每条对角线上的三个数之和都相等;
(3)图3是一个三阶幻方,那么标有x的方格中所填的数是 ;
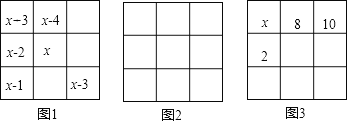
(4)如图4所示的每一个圆中分别填写了1、2、3…19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x= ,y= .

相关试题

