【题目】已知:如图:△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O. 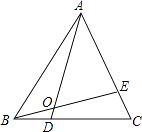
(1)求证:△ACD≌△BAE;
(2)求∠AOB的度数.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,BC=AC,
∵BD=CE,
∴BC﹣BD=AC﹣CE,
∴AE=CD,
在△ACD和△BAE中

∴△ACD≌△BAE(SAS)
(2)解:∵△ACD≌△BAE,
∴∠CAD=∠ABE,
∴∠AOE=∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°,
∴∠AOB=180°﹣60°=120°
【解析】(1)根据等边三角形的性质求出∠BAC=∠C=60°,AC=BC,求出AE=CD,根据SAS推出全等即可;(2)根据全等三角形的性质求出∠CAD=∠ABE,根据三角形外角性质求出∠AOE=∠BAC=60°,即可得出答案.
【考点精析】通过灵活运用三角形的外角和等边三角形的性质,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等边三角形的三个角都相等并且每个角都是60°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.
(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据:
 ≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )
A.y=5(x+2)2+3
B.y=5(x﹣2)2+3
C.y=5(x﹣2)2﹣3
D.y=5(x+2)2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
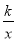 (k≠0)的图象经过点(8,-
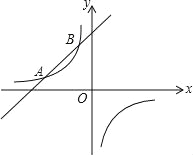
(k≠0)的图象经过点(8,-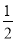 ),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).(1)求上述反比例函数和直线的解析式;
(2)当y1<y2时,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导低碳交通,方便市民出行,某市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费,小聪同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费与使用时间之间存在一次函数的关系.
(1)设使用自行车的费用为y元,使用时间为x小时(x为大于1的整数),求y与x的函数解析式;
(2)若小聪此次使用公共自行车6小时,则她应付多少元费用?
(3)若小聪此次使用公共自行车付费7元,请说明她所使用的时间的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过A(0,3),B(2,3)两点.请你写出一组满足条件的a,b的对应值.a= , b= .
相关试题

