【题目】为了倡导低碳交通,方便市民出行,某市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费,小聪同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费与使用时间之间存在一次函数的关系.
(1)设使用自行车的费用为y元,使用时间为x小时(x为大于1的整数),求y与x的函数解析式;
(2)若小聪此次使用公共自行车6小时,则她应付多少元费用?
(3)若小聪此次使用公共自行车付费7元,请说明她所使用的时间的范围.
参考答案:
【答案】
(1)解:设y与x的函数解析式为y=kx+b,
![]() ,得
,得 ![]() ,
,
即y与x的函数解析式是y=x﹣1
(2)解:当x=6时,y=6﹣1=5,
即若小聪此次使用公共自行车6小时,则她应付5元费用
(3)解:当y=7时,7=x﹣1,得x=8,
∴小聪此次使用公共自行车付费7元,说明她所使用的时间的范围是7<x≤8
【解析】(1)根据题意设出y与x之间的函数关系式,然后根据题目中的数据即可求得y与x的函数解析式;(2)将x=6代入(1)中的函数关系式即可解答本题;(3)将y=7代入(1)中的函数关系式和根据题意可以写出她所使用的时间的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )
A.y=5(x+2)2+3
B.y=5(x﹣2)2+3
C.y=5(x﹣2)2﹣3
D.y=5(x+2)2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
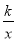 (k≠0)的图象经过点(8,-
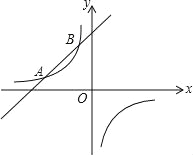
(k≠0)的图象经过点(8,-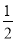 ),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).(1)求上述反比例函数和直线的解析式;
(2)当y1<y2时,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图:△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O.
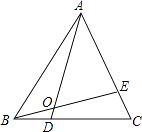
(1)求证:△ACD≌△BAE;
(2)求∠AOB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过A(0,3),B(2,3)两点.请你写出一组满足条件的a,b的对应值.a= , b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.
(1)这个班有多少学生?
(2)这批图书共有多少本?
相关试题

