【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度移动,设运动的时间为
的速度移动,设运动的时间为![]() 秒.
秒.
(1)求![]() 边的长;
边的长;
(2)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值;
的值;
(3)当![]() 为轴对称图形时,求
为轴对称图形时,求![]() 的值.
的值.

参考答案:
【答案】(1)4cm;(2)当![]() 为直角三角形时,t=4或
为直角三角形时,t=4或![]() ;(3)当
;(3)当![]() 为轴对称图形时,t=8或5或
为轴对称图形时,t=8或5或![]()
【解析】
(1)利用勾股定理即可求出结论;
(2)由题意可得:BC=tcm,∠B≠90°,然后根据直角三角形直角的情况分类讨论,利用勾股定理等知识即可解答;
(3)当![]() 为轴对称图形时,△ABP必是等腰三角形,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
为轴对称图形时,△ABP必是等腰三角形,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
解:(1)∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴BC=![]()
(2)由题意可得:BC=tcm,∠B≠90°
当∠APB=90°时,易知点P与点C重合
∴BP = BC
即t=4;
当∠PAB=90°时,如下图所示
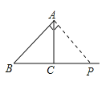
∴CP=BP-BC=(t-4)cm
∵AC2+CP2=AP2=BP2-AB2
∴32+(t-4)2=t2-52
解得:t=![]()
综上:当![]() 为直角三角形时,t=4或
为直角三角形时,t=4或![]() ;
;
(3)当![]() 为轴对称图形时,△ABP必是等腰三角形
为轴对称图形时,△ABP必是等腰三角形
当AB=AP时,如下图所示
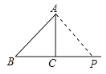
∵AC⊥BC
∴BP=2BC
即t=2×4=8
当AB=BP时,如下图所示

∴t=5;
当AP=BP时,如下图所示
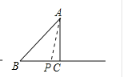
则CP=BC-BP=(4-t)cm,AP=BP=t
在Rt△APC中,![]()
即![]()
解得:t=![]()
综上:当![]() 为轴对称图形时,t=8或5或
为轴对称图形时,t=8或5或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为( )
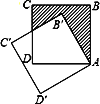
A.
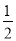 B.
B. 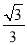 C.
C.  D.
D. 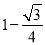
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
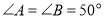 ,
,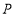 为
为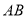 的中点,点
的中点,点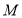 为射线
为射线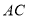 上(不与点
上(不与点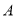 重合)的任意一点,连接
重合)的任意一点,连接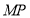 ,并使
,并使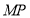 的延长线交射线
的延长线交射线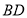 于点
于点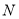 ,设
,设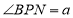 .
.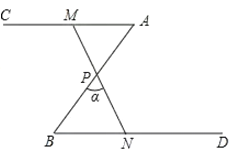
(1)求证:
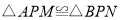 ;
;(2)当
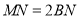 时,求
时,求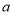 的度数;
的度数;(3)若
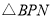 的三边垂直平分线的交点在该三角形的内部,直接写出
的三边垂直平分线的交点在该三角形的内部,直接写出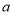 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
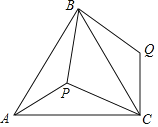
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
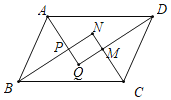
相关试题

