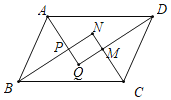
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
参考答案:
【答案】四边形MNPQ是矩形,理由见解析.
【解析】
可得出一个结论,即“四边形PQMN为矩形”.因为平行四边形中邻角互补,所以其每两个相邻内角的平分线都互相垂直,从而根据有三个角是直角的四边形是矩形来判定.
四边形MNPQ是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°,
∵AP,BN分别平分∠DAB,∠ABC,
∴∠PAB+∠PBA=![]() (∠DAB+∠ABC)=×180°=90°,
(∠DAB+∠ABC)=×180°=90°,
∴∠NPQ=∠APB=90°,
同理:∠N=90°,∠AQD=90°,
∴四边形MNPQ是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中, ,
, ,
, ,动点
,动点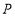 从点
从点 出发沿射线
出发沿射线 以
以 的速度移动,设运动的时间为
的速度移动,设运动的时间为 秒.
秒.(1)求
 边的长;
边的长;(2)当
 为直角三角形时,求
为直角三角形时,求 的值;
的值;(3)当
 为轴对称图形时,求
为轴对称图形时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

-
科目: 来源: 题型:
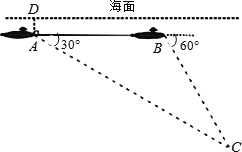
查看答案和解析>>【题目】如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
A. 2000米 B. 4000米 C. 2000米 D. (2000
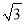 +500)米
+500)米
相关试题

