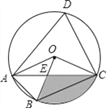
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2![]() ,则图中阴影部分面积是_____(结果保留π和根号)
,则图中阴影部分面积是_____(结果保留π和根号)
参考答案:
【答案】3π﹣2![]()
【解析】∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC﹣∠AOB=90°,
在Rt△OCE中,OC=2![]() ,
,
∴OE=OCtan∠OCE=2![]() tan30°=2
tan30°=2![]() ×
×![]() =2,
=2,
∴S△OEC=![]() OEOC=
OEOC=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∴S扇形OBC=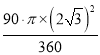 =3π,
=3π,
∴S阴影=S扇形OBC﹣S△OEC=3π﹣2![]() .
.
故答案为:3π﹣2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20
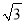 米.
米.(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
-
科目: 来源: 题型:
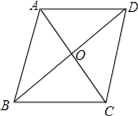
查看答案和解析>>【题目】如图,在
 ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
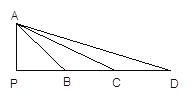
A. ΔPAB∽ΔPDA B. ΔABC∽ΔDCA
C. ΔPAB∽ΔPCA D. ΔABC∽ΔDBA
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了知道一张课桌所占的空间,应该通过测量收集数据,包括课桌的 、 和 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣ab2)3的结果是( )
A.a3b5
B.﹣a3b5
C.﹣a3b6
D.a3b6 -
科目: 来源: 题型:
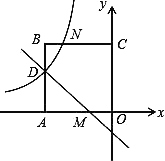
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =
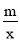 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
相关试题

