【题目】如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
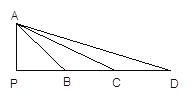
A. ΔPAB∽ΔPDA B. ΔABC∽ΔDCA
C. ΔPAB∽ΔPCA D. ΔABC∽ΔDBA
参考答案:
【答案】D
【解析】根据相似三角形的判定,采用排除法,逐条分析判断.
解:∵∠APD=90°,
而∠PAB≠∠PCB,∠PBA≠∠PAC,
∴无法判定△PAB与△PCA相似,故A错误;
同理,无法判定△PAB与△PDA,△ABC与△DCA相似,故B、D错误;
∵∠APD=90°,AP=PB=BC=CD,
∴AB=![]() PA,AC=
PA,AC=![]() PA,AD=
PA,AD=![]() PA,BD=2PA,
PA,BD=2PA,
∴![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴△ABC∽△DBA,故D正确.
故选D.
本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果你要购买一枝钢笔,你最关心 .
-
科目: 来源: 题型:
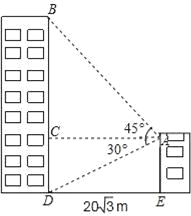
查看答案和解析>>【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20
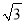 米.
米.(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
-
科目: 来源: 题型:
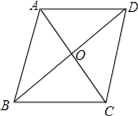
查看答案和解析>>【题目】如图,在
 ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
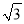 ,则图中阴影部分面积是_____(结果保留π和根号)
,则图中阴影部分面积是_____(结果保留π和根号)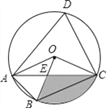
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了知道一张课桌所占的空间,应该通过测量收集数据,包括课桌的 、 和 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣ab2)3的结果是( )
A.a3b5
B.﹣a3b5
C.﹣a3b6
D.a3b6
相关试题

