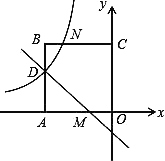
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
参考答案:
【答案】(1) 反比例解析式为y=﹣![]() ,则直线DM解析式为y=﹣x﹣1;(2)P坐标为(﹣10,9)或(8,﹣9).
,则直线DM解析式为y=﹣x﹣1;(2)P坐标为(﹣10,9)或(8,﹣9).
【解析】试题分析:(1)由正方形OABC的顶点C坐标,确定出边长,及四个角为直角,根据AD=2DB,求出AD的长,确定出D坐标,代入反比例解析式求出m的值,再由AM=2MO,确定出MO的长,即M坐标,将M与D坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)把y=3代入反比例解析式求出x的值,确定出N坐标,得到NC的长,设P(x,y),根据△OPM的面积与四边形OMNC的面积相等,求出y的值,进而得到x的值,确定出P坐标即可.
试题解析:(1)∵正方形OABC的顶点C(0,3),
∴OA=AB=BC=OC=3,∠OAB=∠B=∠BCO=90°,
∵AD=2DB,
∴AD=![]() AB=2,
AB=2,
∴D(﹣3,2),
把D坐标代入y=![]()
![]() 得:m=﹣6,
得:m=﹣6,
∴反比例解析式为y=﹣![]() ,
,
∵AM=2MO,
∴MO=![]() OA=1,即M(﹣1,0),
OA=1,即M(﹣1,0),
把M与D坐标代入y=kx+b中得: ![]()
![]() ,
,
解得:k=b=﹣1,
则直线DM解析式为y=﹣x﹣1;
(2)把y=3代入y=﹣![]() 得:x=﹣2,
得:x=﹣2,
∴N(﹣2,3),即NC=2,
设P(x,y),
∵△OPM的面积与四边形OMNC的面积相等,
∴![]()
![]() (OM+NC)OC=
(OM+NC)OC=![]() OM|y|,即|y|=9,
OM|y|,即|y|=9,
解得:y=±9,
当y=9时,x=﹣10,当y=﹣9时,x=8,
则P坐标为(﹣10,9)或(8,﹣9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
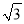 ,则图中阴影部分面积是_____(结果保留π和根号)
,则图中阴影部分面积是_____(结果保留π和根号)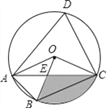
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了知道一张课桌所占的空间,应该通过测量收集数据,包括课桌的 、 和 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣ab2)3的结果是( )
A.a3b5
B.﹣a3b5
C.﹣a3b6
D.a3b6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD=AB=BC,那么∠1和∠2之间的关系是( )

A.∠1=∠2
B.2∠1+∠2=180°
C.∠1+3∠2=180°
D.3∠1-∠2=180° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不具有稳定性的图形是( )
A. 平行四边形 B. 等腰三角形 C. 直角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 无限小数是无理数;B. 实数可分为有理数和无理数;
C. 任何数都有平方根;D. 零没有平方根
相关试题

