【题目】某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式.
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
参考答案:
【答案】
(1)解:经过图表数据分析,每天售出件数y与每件售价x(元)之间的函数关系为一次函数,
设y=kx+b,经过(50,300)、(60,240),
![]() ,
,
解得k=﹣6,b=600,
故y=﹣6x+600
(2)解:①设每件产品应定价x元,由题意列出函数关系式
W=(x﹣40)×(﹣6x+600)﹣3×40
=﹣6x2+840x﹣24000﹣120
=﹣6(x2﹣140x+4020)
=﹣6(x﹣70)2+5280.
②当y=168时x=72,这时只需要两名员工,
W=(72﹣40)×168﹣80=5296>5280.
故当每件产品应定价72元,才能使每天门市部纯利润最大
【解析】(1)经过图表数据分析,每天售出件数y与每件售价x(元)之间的函数关系为一次函数,设y=kx+b,解出k、b即可求出;(2)由利润=(售价﹣成本)×售出件数﹣工资,列出函数关系式,求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图是在同一直角坐标系内,二次函数y=ax2+(a+c)x+c与一次函数y=ax+c的大致图象,有且只有一个是正确的,正确的是( )
A.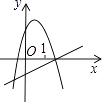
B.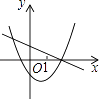
C.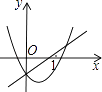
D.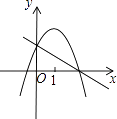
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m满足m2﹣m﹣2=0,当m=时,函数y=xm+(m+1)x+m+1的图象与x轴无交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx﹣2(k>0)与双曲线
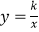 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 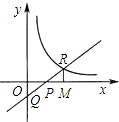
-
科目: 来源: 题型:
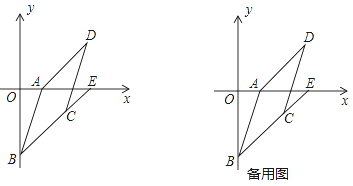
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移得到BC,使B(0,b),且a,b满足|a﹣2|+
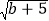 =0,延长BC交x轴于点E.
=0,延长BC交x轴于点E.(1)填空:点A( , ),点B( , ),∠DAE= ;
(2)求点C和点E的坐标;
(3)设点P是x轴上的一动点(不与点A、E重合),且PA>AE,探究∠APC与∠PCB的数量关系?写出你的结论并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一单杆高2.2m,两立柱之间的距离为1.6m,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.
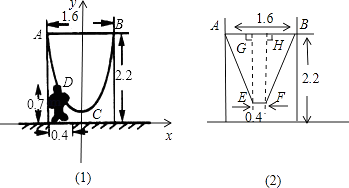
(1)一身高0.7m的小孩站在离立柱0.4m处,其头部刚好触上绳子,求绳子最低点到地面的距离;
(2)为供孩子们打秋千,把绳子剪断后,中间系上一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,求这时木板到地面的距离.(供选用数据: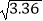 ≈1.8,
≈1.8, 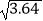 ≈1.9,
≈1.9, 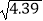 ≈2.1)
≈2.1) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图是在同一直角坐标系内,二次函数y=ax2+(a+c)x+c与一次函数y=ax+c的大致图象,有且只有一个是正确的,正确的是( )
A.
B.
C.
D.
相关试题

