【题目】已知:在等边△ABC中, AB= ![]() ,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
(1)判断△BDE的形状;
(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为 . (直接填写结果)
参考答案:
【答案】
(1)解:∵D,E分别是AB,BC的中点,
∴DE= ![]() BC,BD=
BC,BD= ![]() BA,
BA,
∵△ABC为等边三角形,
∴∠B=60°,BA=BC,
∴BD=BE,
∴△BDE为等边三角形
(2)解:补全图形如图2所示:
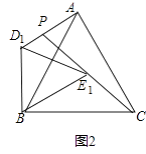
①CE1=AD1.理由如下:
∵△BDE绕点B逆时针旋转,得到△BD1E1,
∴△BD1E1为等边三角形,
∴BD1=BE1,∠D1BE1=60°,
而∠ABC=60°,
∴∠ABD1=∠CBE1,
∴△ABD1可由△CBE1绕点B逆时针旋转得到,
∴CE1=AD1;
②∵△ABD1可由△CBE1绕点B逆时针旋转得到,
∴∠BAD1=∠BCE1,
∴∠APC=∠ABC=60°
(3)6
【解析】(3)解:∵∠APC=∠D1BE1=60°,
∴点P、D1、B、E1共圆,
∴当BP⊥BC时,点P到BC所在直线的距离的最大值,此时点E1在AB上,
在Rt△PBC中,PB= ![]() AB=
AB= ![]() ×2
×2 ![]() =2,
=2,
∴点P到BC所在直线的距离的最大值为2.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车出发前油箱中有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
(1)机动车行驶了 小时后加油,加油 升;
(2)加油后油箱中的油最多可行驶多少小时?
(3)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去,若OA=OB=1.
(1)A1B=________,S△A1B1A2=________;
(2)试猜想第n个等腰直角三角形的面积Sn.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1 , y2 , 都有点(x,y1)、(x,y2)关于点(x,x)对称,则称这两个函数为关于y=x的对称函数.例如,
 和
和 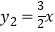 为关于y=x的对称函数.
为关于y=x的对称函数.
(1)判断:① 和
和 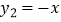 ;②
;② 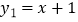 和
和 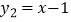 ;③
;③ 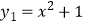 和
和 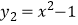 ,其中为关于y=x的对称函数的是(填序号).
,其中为关于y=x的对称函数的是(填序号).
(2)若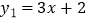 和
和 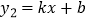 (
( 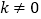 )为关于y=x的对称函数.
)为关于y=x的对称函数.
①求k、b的值.
②对于任意的实数x,满足x>m时,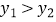 恒成立,则m满足的条件为 .
恒成立,则m满足的条件为 .
(3)若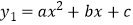
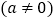 和
和 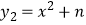 为关于y=x的对称函数,且对于任意的实数x,都有
为关于y=x的对称函数,且对于任意的实数x,都有 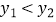 ,请结合函数的图象,求n的取值范围.
,请结合函数的图象,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?

相关试题

