【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围.
参考答案:
【答案】
(1)证明:△=64m2-4m(16m-1)
=4m,
∵m>0,
∴△>0,
∴抛物线总与x轴有两个不同的交点
(2)解:根据题意,x1、x2为方程mx2-8mx+16m-1=0的两根,
∴x1+x2=- ![]() =8,x1x2=
=8,x1x2= ![]() ,
,
∵|x1-x2|=2,
∴(x1+x2)2-4x1x2=4,
∴82-4 ![]() =4,
=4,
∴m=1,
∴抛物线的解析式为y=x2-8x+15
(3)解:抛物线的对称轴为直线x=- ![]() =4,
=4,
∵抛物线开口向上,
∴当x=2,y≥0时,抛物线与线段CD有交点,
∴4m-16m+16m-1≥0,
∴m≥ ![]()
【解析】(1)证抛物线与x轴交点个数可转化为计算判别式,判断判别式的正负来判定交点个数;(2)AB可转化为两根之差,再利用根与系数关系求解;(3)要使抛物线与线段CD有交点,需x=2,y≥0,构建不等式4m-16m+16m-1≥0,可求出范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中, AD是角平分线.
求证: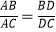 .
.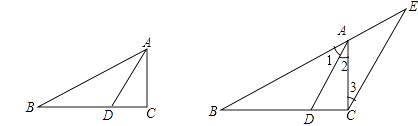
证明:过C作CE∥DA,交BA的延长线于E.
∴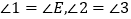 . ①
. ① AD是角平分线,
AD是角平分线,
∴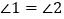 .
.
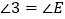 .
.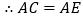 . ②
. ②
又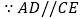 ,
,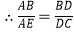 . ③
. ③
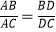 .
.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABD和△ACD面积的比来证明三角形内角平分线定理. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.
 B.3 C.1 D.
B.3 C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.

⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;
⑵你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①画出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车出发前油箱中有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
(1)机动车行驶了 小时后加油,加油 升;
(2)加油后油箱中的油最多可行驶多少小时?
(3)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在等边△ABC中, AB=
 ,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
(1)判断△BDE的形状;
(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为 . (直接填写结果)
相关试题

