【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100( ![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
参考答案:
【答案】
(1)
解:如图,作CE⊥AB于E,
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AEtan60°= ![]() x;
x;
在Rt△BCE中,BE=CE= ![]() x.
x.
∴AE+BE=x+ ![]() x=100(
x=100( ![]() +1),
+1),
解得:x=100.
AC=2x=200.
在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°.
过点D作DF⊥AC于点F,
设AF=y,则DF=CF= ![]() y,
y,
∴AC=y+ ![]() y=200,
y=200,
解得:y=100( ![]() ﹣1),
﹣1),
∴AD=2y=200( ![]() ﹣1).
﹣1).

答:A与C之间的距离AC为200海里,A与D之间的距离AD为200( ![]() ﹣1)海里.
﹣1)海里.
(2)
解:由(1)可知,DF= ![]() AF=
AF= ![]() ×100(
×100( ![]() ﹣1)≈126.3海里,
﹣1)≈126.3海里,
因为126.3>100,所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险.
【解析】(1)作CE⊥AB于E,设AE=x海里,则BE=CE= ![]() x海里.根据AB=AE+BE=x+
x海里.根据AB=AE+BE=x+ ![]() x=100(
x=100( ![]() +1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;(2)根据(1)中的结论得出DF的长,再与100比较即可得到答案.
+1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;(2)根据(1)中的结论得出DF的长,再与100比较即可得到答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率. -
科目: 来源: 题型:
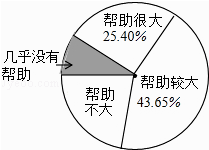
查看答案和解析>>【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成).
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1) -
科目: 来源: 题型:
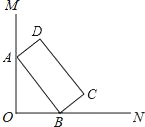
查看答案和解析>>【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A.
 +1 B.
+1 B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A,O,B分别表示-16,0,14,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.若点P,Q,O三点在运动过程中,其中一点恰好是另外两点为端点构成的线段的三等分点时,则运动时间为_秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.

(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
(1)∠DCF+
 ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.其中一定成立的是_____(把所有正确结论的序号都填在横线上)

相关试题

