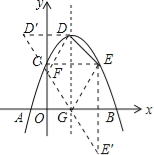
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+x2>2,则y1> y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为![]() .其中正确判断的序号是( )
.其中正确判断的序号是( )

A. ① B. ② C. ③ D. ④
参考答案:
【答案】C
【解析】试题分析:①根据二次函数所过象限,判断出y的符号;
②根据A、B关于对称轴对称,求出b的值;
③根据![]() >1,得到x1<1<x2,从而得到Q点距离对称轴较远,进而判断出y1>y2;
>1,得到x1<1<x2,从而得到Q点距离对称轴较远,进而判断出y1>y2;
④作D关于y轴的对称点D′,E关于x轴的对称点E′,连接D′E′,D′E′与DE的和即为四边形EDFG周长的最小值.求出D、E、D′、E′的坐标即可解答.
解:①当x>0时,函数图象过一四象限,当0<x<b时,y>0;当x>b时,y<0,故本选项错误;
②二次函数对称轴为x=﹣![]() =1,当a=﹣1时有
=1,当a=﹣1时有![]() =1,解得b=3,故本选项错误;
=1,解得b=3,故本选项错误;
③∵x1+x2>2,
∴![]() >1,
>1,
又∵x1﹣1<1<x2﹣1,
∴Q点距离对称轴较远,
∴y1>y2,故本选项正确;
④如图,作D关于y轴的对称点D′,E关于x轴的对称点E′,
连接D′E′,D′E′与DE的和即为四边形EDFG周长的最小值.
当m=2时,二次函数为y=﹣x2+2x+3,顶点纵坐标为y=﹣1+2+3=4,D为(1,4),则D′为(﹣1,4);C点坐标为C(0,3);则E为(2,3),E′为(2,﹣3);
则DE=![]() =
=![]() ;D′E′=
;D′E′=![]() =
=![]() ;
;
∴四边形EDFG周长的最小值为![]() +
+![]() ,故本选项错误.
,故本选项错误.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形,是因式分解的是( )
A.3x(x+y)+3x2+3xy
B.﹣2x2﹣2xy=﹣2x(x+y)
C.(x+5)(x﹣5)=x2﹣25
D.x2+x+1=x(x+1)+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
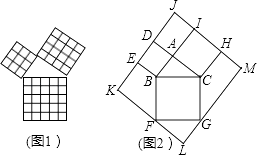
A.90
B.100
C.110
D.121 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(mx4)·(4xk)=-12x12,则适合条件的m,k的值分别是( )
A. m=-3,k=8 B. m=3,k=8
C. m=8,k=3 D. m=-3,k=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+4是一个完全平方式,则常数k的值为()
A. 4 B. -4 C. ±4 D. ±2
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

相关试题

