【题目】如图,直线BC//OA,∠C=∠OAB=100°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值(提示:图中∠OFC=∠BOF+∠OBC);
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数;若不存在,说明理由(提示:三角形三个内角的和为180).

参考答案:
【答案】(1)40°;(2)∠OBC:∠OFC=1:2,是定值;(3)∠OEC=∠OBA=60°
【解析】试题分析:(1)根据两直线平行,同旁内角互补求出∠AOC,然后求出∠EOB=![]() ∠AOC,计算即可得解;
∠AOC,计算即可得解;
(2)根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠OFC=2∠OBC,从而得解;
(3)根据三角形的内角和定理求出∠COE=∠AOB,从而得到OB、OE、OF是∠AOC的四等分线,再利用三角形的内角和定理列式计算即可得解.
试题解析:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=0.5∠AOC=0.5×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=0.25∠AOC=0.25×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
A.已知①②则③B.已知②⑤则④C.已知②④则③D.已知④⑤则②
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,Rt△ABC中,∠BAC=90°
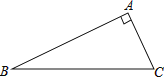
(1)按要求作图:(保留作图痕迹)
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段 AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A为数轴上表示2的点,将点A沿数轴向左平移5个单位到点B,则点B所表示的数的绝对值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表中的信息解决问题:

若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是( )
A.±2B.﹣2C.2D.不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90.解答下列问题:
(1) 如果AB=AC,∠BAC=90.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?

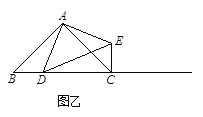
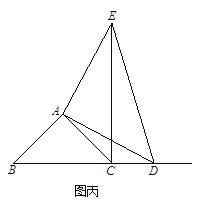
(2) 如果AB≠AC,∠BAC≠90,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
相关试题

