Question

【题目】如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作等腰直角三角形ADE，AD=AE，∠DAE=90.解答下列问题：

(1) 如果AB=AC，∠BAC=90．

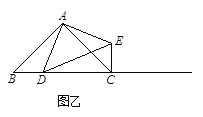
①当点D在线段BC上时（与点B不重合），如图乙，线段CE、BD之间的位置关系为，数量关系为．（不用证明）

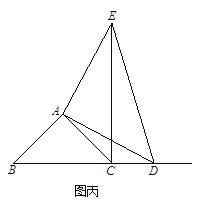
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

(2) 如果AB≠AC，∠BAC≠90，点D在线段BC上运动．

试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）？画出相应的图形，并说明理由．

Answer 1

【答案】见解析

【解析】试题分析：（1）①根据∠BAD=∠CAE，BA=CA，AD=AE，运用“SAS”证明△ABD≌△ACE，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE、BD之间的关系；②先根据“SAS”证明△ABD≌△ACE，再根据全等三角形性质得出对应边相等，对应角相等，即可得到①中的结论仍然成立；

（2）先过点A作AG⊥AC交BC于点G，画出符合要求的图形，再结合图形判定△GAD≌△CAE，得出对应角相等，即可得出结论．

试题解析：（1）①CE与BD位置关系是CE⊥BD，数量关系是CE=BD.

理由：如图乙,

∵∠BAD=90°∠DAC,∠CAE=90°∠DAC，

∴∠BAD=∠CAE.

又BA=CA，AD=AE，

∴△ABD≌△ACE(SAS)

∴∠ACE=∠B=45°且CE=BD.

∵∠ACB=∠B=45°，

∴∠ECB=45°+45°=90°，即CE⊥BD.

故答案为：CE⊥BD；CE=BD.

②当点D在BC的延长线上时,①的结论仍成立.

如图丙,

∵∠DAE=90°,∠BAC=90°，

∴∠DAE=∠BAC，

∴∠DAB=∠EAC，

又AB=AC，AD=AE，

∴△DAB≌△EAC，

∴CE=BD，且∠ACE=∠ABD.

∵∠BAC=90°，AB=AC，

∴∠ABC=45°，

∴∠ACE=45°，

∴∠BCE=∠ACB+∠ACE=90°，

即CE⊥BD；

（2）如图丁所示,当∠BCA=45°时,CE⊥BD.

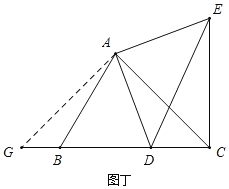
理由：过点A作AG⊥AC交BC于点G，

∴AC=AG,∠AGC=45°，

即△ACG是等腰直角三角形，

∵∠GAD+∠DAC=90°=∠CAE+∠DAC，

∴∠GAD=∠CAE，

又∵DA=EA，

∴△GAD≌△CAE，

∴∠ACE=∠AGD=45°，

∴∠BCE=∠ACB+∠ACE=90°，

即CE⊥BD.