【题目】如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1
B.1∶2∶3
C.2∶3∶4
D.3∶4∶5
参考答案:
【答案】C
【解析】解:过点O作OE⊥AB于点E,OF⊥BC于点F,OD⊥AC于点D,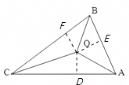
∵OA,OB,OC分别是△ABC三内角的角平分线,
∴OE=OF=OD ,
∵S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,
AC·OD=20OD,
∴S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4
故应选:C.
根据角平方线上的点到角两边的距离相等得出OE=OF=OD ,根据三角形的面积法,得出S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。
AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是尺规作图的痕迹,下列说法不正确的是( )

A.AE,BF是△ABC的内角平分线
B.CG也是△ABC的一条内角平分线
C.点O到△ABC三边的距离相等
D.AO=BO=CO -
科目: 来源: 题型:
查看答案和解析>>【题目】每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).
(1)补全条形统计图和扇形统计图;
(2)若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .
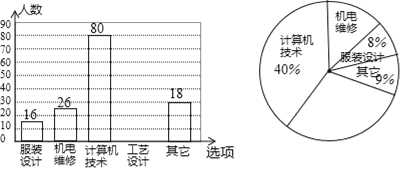
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有 种租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣3)+4的结果是( )
A.﹣7
B.﹣1
C.1
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC,∠ACB的平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )
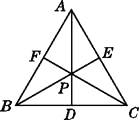
A.直角三角形
B.等边三角形
C.等腰三角形
D.等腰直角三角形
相关试题

