【题目】如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为 ![]() ,CD=4,则弦AC的长为( )
,CD=4,则弦AC的长为( ) 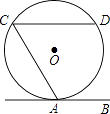
A.2 ![]()
B.3 ![]()
C.4
D.2 ![]()
参考答案:
【答案】A
【解析】解:连接AO并延长,交CD于点E,连接OC, ∵直线AB与⊙O相切于点A,
∴EA⊥AB,
∵CD∥AB,
∠CEA=90°,
∴AE⊥CD,
∴CE= ![]() CD=
CD= ![]() ×4=2,
×4=2,
∵在Rt△OCE中,OE= ![]() =
= ![]() ,
,
∴AE=OA+OE=4,
∴在Rt△ACE中,AC= ![]() =2
=2 ![]() .
.
故选A.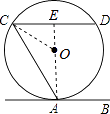
【考点精析】本题主要考查了垂径定理和切线的性质定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
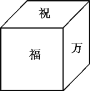
A.
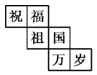 B.
B. 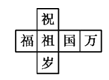 C.
C. 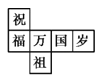 D.
D. 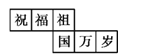
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
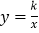 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y=ax+b经过点A,并且经过反比例函数的图象上另一点C(n,-2).
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y=ax+b经过点A,并且经过反比例函数的图象上另一点C(n,-2).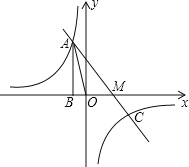
(1)求反比例函数
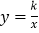 与直线y=ax+b的解析式;
与直线y=ax+b的解析式;(2)连接OC,求△AOC的面积;
(3)根据所给条件,直接写出不等式
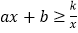 的解集
的解集 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4
 )-(-5
)-(-5 )+(-4
)+(-4 )-3
)-3 ;
;(3)
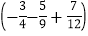 ÷
÷ ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)× .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
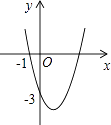
A.﹣3<P<﹣1
B.﹣6<P<0
C.﹣3<P<0
D.﹣6<P<﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 .
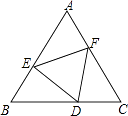
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 .
相关试题

