【题目】如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF.
(2)若∠A=65°,求∠AGF的度数.

参考答案:
【答案】(1)见解析;(2) 50o
【解析】
(1)先由BF=CE得到BC=EF,再根据HL证明△ABC≌△DEF;
(2)在Rt△ABC中求得∠ACB=25o,再由三角形全等得到∠DFE=25o,再根据三角形外角的性质求得∠AGF的度数.
(1)∵BF=CE,
∴BF+FC=EC+CF,即BC=EF,
∵AB⊥BE,垂足为B,DE⊥BE,垂足为E,
∴△ABC和△DEF是直角三角形,
在Rt△ABC和Rt△DEF中,
![]() ,
,
∴Rt△ABC≌Rt△DEF(HL);
(2) 在Rt△ABC中,∠A=65°,
∴∠ACB=25o,
又∵Rt△ABC≌Rt△DEF,
∴∠DFE=∠ACB=25o,
又∵∠AGF=∠DFE+∠ACB,
∴∠AGF=50o.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:有一块三角形状的土地平均分给四户人家,现有四种不同的分法,
 如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点
如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点 ,其中正确的分法有
,其中正确的分法有


A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,则AB=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
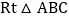 中,
中, ,
, ,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将
,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将 绕点B时针旋转,使点A旋转至y轴的正半轴上的A处
绕点B时针旋转,使点A旋转至y轴的正半轴上的A处 则图中阴影部分的面积为______
则图中阴影部分的面积为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将
,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将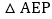 沿着边PE折叠,折叠后得到
沿着边PE折叠,折叠后得到 ,当折叠后
,当折叠后 与
与 的重叠部分的面积恰好为
的重叠部分的面积恰好为 面积的四分之一,则此时BP的长为______.
面积的四分之一,则此时BP的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织
 名同学和
名同学和 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为 人/辆,小客车载客量为
人/辆,小客车载客量为 人/辆
人/辆(1)学校准备租用
 辆客车,有几种租车方案?
辆客车,有几种租车方案?(2)在(1)的条件下,若大客车租金为
 元/辆,小客车租金为
元/辆,小客车租金为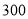 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?(3)学校临时增加
 名学生和
名学生和 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有 人,请你帮助设计租车方案
人,请你帮助设计租车方案
相关试题

