Question

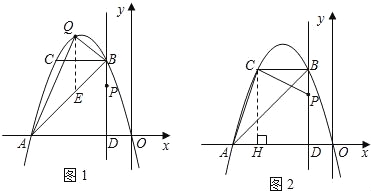
【题目】如图，经过原点的抛物线y=﹣x2﹣2mx（m＞1）与x轴的另一个交点为A．过点P（﹣1，m）作直线PD⊥x轴于点D，交抛物线于点B，BC∥x轴交抛物线于点C．

（1）当m=2时．

①求线段BC的长及直线AB所对应的函数关系式；

②若动点Q在直线AB上方的抛物线上运动，求点Q在何处时，△QAB的面积最大？

③若点F在坐标轴上，且PF=PC，请直接写出符合条件的点F在坐标；

（2）当m＞1时，连接CA、CP，问m为何值时，CA⊥CP？

Answer 1

【答案】（1）①直线AB所对应的函数关系式为y=x+4；

②当a=-时，△QAB的面积最大，此时Q的坐标为（-，）；

③符合条件的点F坐标为F1（﹣2，0），F2（0，0），F3（0，4）；

（2）m=．

【解析】

试题分析：（1）①将m=2代入y=﹣x2﹣2mx，得出y=﹣x2﹣4x，求出A（﹣4，0），B（﹣1，3），由B、C两点关于抛物线y=﹣x2﹣4x的对称轴x=﹣2对称，得出BC=2，运用待定系数法求出直线AB所对应的函数关系式；

②过点Q作QE∥y轴，交AB于点E，设Q（a，﹣a2﹣4a），则E（a，a+4），QE=（﹣a2﹣4a）﹣（a+4）=﹣a2﹣5a﹣4，由S△QAB=QEAD求出S△QAB=﹣（a+）2+，根据二次函数的性质即可求解；

③分两种情况进行讨论：若点F在x轴上，设F（x，0）．根据PF=PC列出方程，解方程得到F1（﹣2，0），F2（0，0）；若点F在y轴上，设F（0，y），根据PF=PC列出方程，解方程得到F3（0，4），F4（0，0）与F2（0，0）重合；

（2）过点C作CH⊥x轴于点H．先求出PB=m﹣1，BC=2（m﹣1），CH=2m﹣1，AH=1，再证明△ACH∽△PCB，根据相似三角形对应边成比例得出，即，解方程可求出m的值．

试题解析：（1）①当m=2时，y=﹣x2﹣4x，

令y=0，得﹣x2﹣4x=0，

解得x1=0，x2=﹣4，

则A（﹣4，0）．

当x=﹣1时，y=3，

则B（﹣1，3）．

∵抛物线y=﹣x2﹣4x的对称轴为直线x=﹣2，

∴B、C两点关于对称轴x=﹣2对称，

∴C（﹣3，3），BC=2．

设直线AB所对应的函数关系式为y=kx+b．

∵A（﹣4，0）、B（﹣1，3）在直线AB上，

∴，解得

∴直线AB所对应的函数关系式为y=x+4；

②过点Q作QE∥y轴，交AB于点E（如图1）．

由题意可设Q（a，﹣a2﹣4a），则E（a，a+4），

∴QE=（﹣a2﹣4a）﹣（a+4）=﹣a2﹣5a﹣4．

∴S△QAB=QEAD=×（﹣a2﹣5a﹣4）×3=﹣（a+）2+，

∴当a=-时，△QAB的面积最大，此时Q的坐标为（-，）；

③分两种情况：

若点F在x轴上，设F（x，0）．

∵PF=PC，P（﹣1，2），C（﹣3，3），

∴（x+1）2+（2﹣0）2=（﹣3+1）2+（3﹣2）2，

整理，得x2+2x=0，

解得x1=﹣2，x2=0，

∴F1（﹣2，0），F2（0，0）；

若点F在y轴上，设F（0，y）．

∵PF=PC，P（﹣1，2），C（﹣3，3），

∴（0+1）2+（y﹣2）2=（﹣3+1）2+（3﹣2）2，

整理，得y2﹣4y=0，

解得y1=4，y2=0，

∴F3（0，4），F4（0，0）与F2（0，0）重合；

综上所述，符合条件的点F坐标为F1（﹣2，0），F2（0，0），F3（0，4）；

（2）过点C作CH⊥x轴于点H（如图2）．∵P（﹣1，m），B（﹣1，2m﹣1），

∴PB=m﹣1．∵抛物线y=﹣x2﹣2mx的对称轴为直线x=﹣m，其中m＞1，

∴B、C两点关于对称轴x=﹣m对称，∴BC=2（m﹣1），

∴C（1﹣2m，2m﹣1），H（1﹣2m，0），∴CH=2m﹣1，∵A（﹣2m，0），∴AH=1．

由已知，得∠ACP=∠BCH=90°，∴∠ACH=∠PCB．又∵∠AHC=∠PBC=90°，

∴△ACH∽△PCB，∴，即，∴m=．