【题目】如图,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,顶点
上,顶点![]() 、
、![]() 在菱形
在菱形![]() 的对角线
的对角线![]() 上.
上.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 中点,
中点,![]() ,求菱形
,求菱形![]() 的周长。
的周长。
参考答案:
【答案】(1)证明见解析;(2)8.
【解析】
(1)根据矩形的性质得到EH=FG,EH∥FG,得到∠GFH=∠EHF,求得∠BFG=∠DHE,根据菱形的性质得到AD∥BC,得到∠GBF=∠EDH,根据全等三角形的性质即可得到结论;
(2)连接EG,根据菱形的性质得到AD=BC,AD∥BC,求得AE=BG,AE∥BG,得到四边形ABGE是平行四边形,得到AB=EG,于是得到结论.
(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
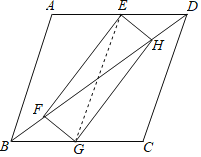
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了乘法公式
 后,老师向同学们提出了如下问题:
后,老师向同学们提出了如下问题:①将多项式x2+4x+3因式分解;
②求多项式x2+4x+3的最小值.

请你运用上述的方法解决下列问题:
(1)将多项式x2+8x-20因式分解;
(2)求多项式x2+8x-20的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,
,  与
与 成正比例,
成正比例,  与
与 成反比例,并且当
成反比例,并且当 时,
时,  ,当
,当 时,
时, 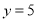 .
.(
 )求
)求 关于
关于 的函数关系式.
的函数关系式.(
 )当
)当 时,求
时,求 的值.
的值.【答案】(
 )
) ;(
;( )
) ,
,  .
.【解析】分析:(1)首先根据
 与x成正比例,
与x成正比例, 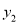 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出 和
和 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.本题解析:
(
 )设
)设 ,
, 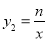 ,
,则
 ,
,∵当
 时,
时,  ,当
,当 时,
时,  ,
,∴

解得,
 ,
,∴
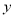 关于
关于 的函数关系式为
的函数关系式为 .
.(
 )把
)把 代入
代入 得,
得, ,
,解得:
 ,
,  .
.点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24【题目】如图,菱形
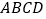 的对角线
的对角线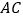 、
、 相交于点
相交于点 ,过点
,过点 作
作 且
且 ,连接
,连接 、
、 ,连接
,连接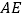 交
交 于点
于点 .
.(1)求证:
 ;
;(2)若菱形
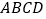 的边长为2,
的边长为2,  .求
.求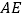 的长.
的长.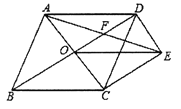
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们定义直线
 为抛物线
为抛物线 、b、c为常数,
、b、c为常数, 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线
 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点 点A在点B的左侧
点A在点B的左侧 ,与x轴负半轴交于点C.
,与x轴负半轴交于点C. 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______; 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标; 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求
 的值;
的值;(3)在(2)的条件下,若
 =k(k为大于
=k(k为大于 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示 的值.
的值.
相关试题

