【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.

(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明).
参考答案:
【答案】(1)证明见解析;
(2)CE、EG、BG之间的数量关系为:CE+BG=EG,证明见解析;
(3)当∠EDG=90°﹣![]() α时, CE+BG=EG仍然成立.
α时, CE+BG=EG仍然成立.
【解析】试题分析:(1)首先判断出∠C=∠DBF,然后根据全等三角形判定的方法,判断出△CDE≌△BDF,即可判断出DE=DF.(2)猜想CE、EG、BG之间的数量关系为:CE+BG=EG.首先根据全等三角形判定的方法,判断出△ABD≌△ACD,即可判断出∠BDA=∠CDA=60°;然后根据∠EDG=60°,可得∠CDE=∠ADG,∠ADE=∠BDG,再根据∠CDE=∠BDF,判断出∠EDG=∠FDG,据此推得△DEG≌△DFG,所以EG=FG,最后根据CE=BF,判断出CE+BG=EG即可.(3)根据(2)的证明过程,要使CE+BG=EG仍然成立,则∠EDG=∠BDA=∠CDA=![]() ∠CDB,即∠EDG=
∠CDB,即∠EDG=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,据此解答即可.
α,据此解答即可.
试题解析:(1):∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°﹣60°﹣120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在△CDE和△BDF中,
 (SAS)
(SAS)
∴△CDE≌△BDF,
∴DE=DF.
(2)解:如图1,连接AD,猜想CE、EG、BG之间的数量关系为:CE+BG=EG.

证明:在△ABD和△ACD中,
 (SSS)
(SSS)
∴△ABD≌△ACD,
∴∠BDA=∠CDA=![]() ∠CDB=
∠CDB=![]() ×120°=60°,
×120°=60°,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得△CDE≌△BDF,
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在△DEG和△DFG中,

∴△DEG≌△DFG,
∴EG=FG,
又∵CE=BF,FG=BF+BG,
∴CE+BG=EG;
(3)解:要使CE+BG=EG仍然成立,
则∠EDG=∠BDA=∠CDA=![]() ∠CDB,
∠CDB,
即∠EDG=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴当∠EDG=90°﹣![]() α时, CE+BG=EG仍然成立.
α时, CE+BG=EG仍然成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场苹果的价格如下表:
购买苹果
(千克)不超过20千克的部分
超过20千克但不超出40千克的部分
超出40千克的部分
每千克的价格
6元
5元
4元
(1)小明第一次购买苹果10千克,需要付费多少元;
小明第二次购买苹果
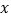 千克(
千克(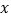 超过20千克但不超过40千克),需要付费多少元(用含
超过20千克但不超过40千克),需要付费多少元(用含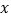 的式子表示);
的式子表示);(2)小强分两次共购买100千克,第二次购买的数量多于第一次购买的数量,且第一次购买的数量为
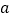 千克,请问小强两次购买苹果共需要付费多少元?(用含
千克,请问小强两次购买苹果共需要付费多少元?(用含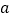 的式子表示);
的式子表示); -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
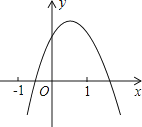
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )
A.9天
B.11天
C.13天
D.22天 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示数-20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记。

比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC......
(1)点A与点C之间的距离记作AC,求AC的长;
若数轴上有一点D满足CD=AD,求D点表示的数;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为
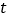 秒.
秒.①若点A向右运动,点C向左运动,AB=BC,求
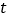 的值.
的值.②若点A向左运动,点C向右运动,
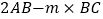 的值不随时间
的值不随时间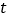 的变化而改变,求
的变化而改变,求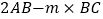 的值.
的值. -
科目: 来源: 题型:
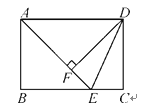
查看答案和解析>>【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
相关试题

