【题目】如图,在数轴上点A表示数-20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记。
![]()
比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC......
(1)点A与点C之间的距离记作AC,求AC的长;
若数轴上有一点D满足CD=AD,求D点表示的数;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为![]() 秒.
秒.
①若点A向右运动,点C向左运动,AB=BC,求![]() 的值.
的值.
②若点A向左运动,点C向右运动,![]() 的值不随时间
的值不随时间![]() 的变化而改变,求
的变化而改变,求![]() 的值.
的值.
参考答案:
【答案】(1)AC=50,D表示5;(2)①t=![]() 或10 ② m=3
或10 ② m=3
【解析】
(1)![]() 数值代入即可,
数值代入即可,![]() 即可求解.
即可求解.
(2)①根据路程=速度x时间,以及两点间的距离公式即;
②根据题意列式得6-2m=0时,由上式的值不随时间t的变化而改变,可得m=3,
(1)![]() ;
;![]() ,D=5.
,D=5.
(2)①如下图所示:

当t=0时,AB=21,BC=29.
下面分两类情况来讨论:
a点A, C在相遇前时,

点A, B之间每秒缩小1个单位长度,点B , C每秒缩小4个单位长度.
在t=0时, BC -AB=8,
如果AB=BC,那么AB-BC=0 ,此时t=![]() 秒,
秒,

b.点A, C在相遇时, AB= BC,
点A,C之间每秒缩小5个单位长度,
在t=0时, AC=50,
t=![]() = 10秒,
= 10秒,
c.点A, C在相遇后,BC大于AC ,不符合条件.
综上所述, t=![]() 或10.
或10.
②当时间为t时,
点A表示得数为-20+2t,
点B表示得数1+t,
点C表示得数为30+3t,![]()
![]() ,
,
当6-2m=0时,上式的值不随时间的变化而改变,此时m=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
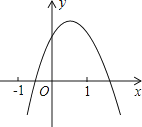
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.

(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )
A.9天
B.11天
C.13天
D.22天 -
科目: 来源: 题型:
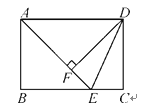
查看答案和解析>>【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣14+
 sin60°+(
sin60°+(  )﹣2﹣(
)﹣2﹣(  )0 .
)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b、c满足(b﹣3)2+|c+4|=0,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
相关试题

