【题目】如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)当t为何值时,△PAE为直角三角形?
(2)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

参考答案:
【答案】(1)t=6,t=![]() ;(2)PA=PE,t=
;(2)PA=PE,t= ![]()
【解析】
(1)需要分类讨论:AE为斜边和AP为斜边两种情况下的直角三角形;
(2)假设存在.利用角平分线的性质,平行线的性质以及等量代换推知:∠PEA=∠EAP,则PE=PA,由此列出关于t的方程,通过解方程求得相应的t的值即可.
(1)∵矩形ABCD中,AB=9,AD=4,
∴CD=AB=9,∠D=90°,
∴DE=9-6=3,
∴AE=![]() =
=![]() =5;
=5;
若∠EPA=90°,t=6;
②若∠PEA=90°,(6-t)2+42+52=(9-t)2,
解得t=![]() .
.
综上所述,当t=6或t=![]() 时,△PAE为直角三角形;
时,△PAE为直角三角形;
(2)假设存在,
∵EA平分∠PED,
∴∠PEA=∠DEA,
∵CD∥AB,
∴∠DEA=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA,
∴(6-t)2+42=(9-t)2,
解得t=![]() .
.
∴满足条件的t存在,此时t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q

(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣
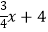 上,则使△ABC是直角三角形的点C的个数为( )
上,则使△ABC是直角三角形的点C的个数为( ) 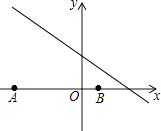
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形
 不是等腰三角形
不是等腰三角形 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念
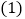 如图1,在
如图1,在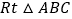 中,
中,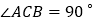 ,
,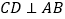 ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形” 概念应用
概念应用 如图2,在
如图2,在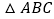 中,CD为角平分线,
中,CD为角平分线, ,
,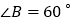 .
.求证:CD为
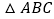 的等角分割线.
的等角分割线.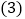 在
在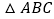 中,
中,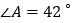 ,CD是
,CD是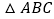 的等角分割线,直接写出
的等角分割线,直接写出 的度数.
的度数.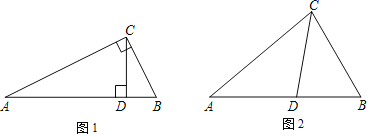
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
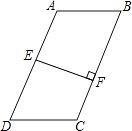
(1)若AB=DC,则四边形ABCD的面积S=;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3)0+|﹣2|﹣
 ÷
÷  +(﹣1)﹣1 .
+(﹣1)﹣1 .
相关试题

