【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.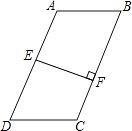
(1)若AB=DC,则四边形ABCD的面积S=;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
参考答案:
【答案】
(1)15
(2)=
【解析】解:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
故答案为:15.
(2)如图,连接EC,延长CD、BE交于点P,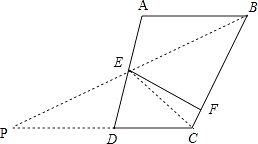
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵ 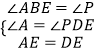 ,
,
∴△ABE≌△DPE(AAS),
∴S△ABE=S△DPE , BE=PE,
∴S△BCE=S△PCE ,
则S四边形ABCD=S△ABE+S△CDE+S△BCE
=S△PDE+S△CDE+S△BCE
=S△PCE+S△BCE
=2S△BCE
=2× ![]() ×BC×EF
×BC×EF
=15,
∴当AB>DC,则此时四边形ABCD的面积S′=S,
故答案为:=.
(1)若AB=DC,则四边形ABCD是平行四边形,据此求出它的面积是多少即可.(2)连接EC,延长CD、BE交于点P,证△ABE≌△DPE可得S△ABE=S△DPE、BE=PE,由三角形中线性质可知S△BCE=S△PCE , 最后结合S四边形ABCD=S△ABE+S△CDE+S△BCE可得答案.此题主要考查了平行四边形的判定和性质的应用及全等三角形的判定与性质,通过构建全等三角形将梯形面积转化为三角形面积去求是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣
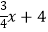 上,则使△ABC是直角三角形的点C的个数为( )
上,则使△ABC是直角三角形的点C的个数为( ) 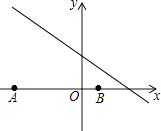
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)当t为何值时,△PAE为直角三角形?
(2)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形
 不是等腰三角形
不是等腰三角形 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念
 如图1,在
如图1,在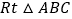 中,
中,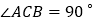 ,
,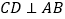 ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形” 概念应用
概念应用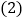 如图2,在
如图2,在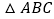 中,CD为角平分线,
中,CD为角平分线, ,
,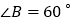 .
.求证:CD为
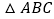 的等角分割线.
的等角分割线.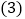 在
在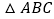 中,
中,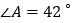 ,CD是
,CD是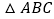 的等角分割线,直接写出
的等角分割线,直接写出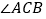 的度数.
的度数.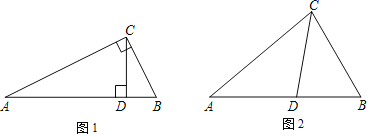
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3)0+|﹣2|﹣
 ÷
÷  +(﹣1)﹣1 .
+(﹣1)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 任意两个矩形一定相似 B. 相似图形就是位似图形
C. 如果
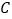 点是线段
点是线段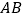 的黄金分割点,那么
的黄金分割点,那么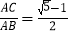 D. 有一个锐角相等的两个直角三角形相似
D. 有一个锐角相等的两个直角三角形相似 -
科目: 来源: 题型:
查看答案和解析>>【题目】初二(
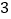 )班的全体同学在体测当天沿着同一条路匀速从名校联中班级教室出发到重庆一中本部操场参加体育测试,行进到本部综合楼时班主任老师发现未带相关体测器材,立即派小赵同学原路匀速跑回本班教室取器材(取器材时间为
)班的全体同学在体测当天沿着同一条路匀速从名校联中班级教室出发到重庆一中本部操场参加体育测试,行进到本部综合楼时班主任老师发现未带相关体测器材,立即派小赵同学原路匀速跑回本班教室取器材(取器材时间为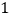 分钟),然后马上又以原速的
分钟),然后马上又以原速的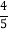 去追赶班级队伍.当途中再次经过综合楼时,小赵发现班级队伍在自己前面不远处,于是他又以之前的速度追赶班级队伍,结果仍然比班级队伍晚
去追赶班级队伍.当途中再次经过综合楼时,小赵发现班级队伍在自己前面不远处,于是他又以之前的速度追赶班级队伍,结果仍然比班级队伍晚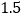 分钟到达本部操场.如图所示,设小赵与本部操场之间距离为
分钟到达本部操场.如图所示,设小赵与本部操场之间距离为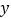 (
(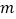 ),小赵所用时间为
),小赵所用时间为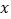 (
(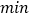 ),则当小赵途中再次经过综合楼时,班级队伍(队伍长度忽略不计)离本部操场的距离是______米.
),则当小赵途中再次经过综合楼时,班级队伍(队伍长度忽略不计)离本部操场的距离是______米.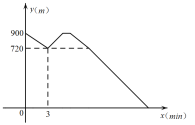
相关试题

