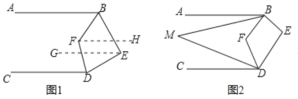
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F,
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.

参考答案:
【答案】![]()
![]() ;
;
![]()
![]() ,证明见解析.
,证明见解析.
![]()
![]() .
.
【解析】
![]() 首先作EG∥AB,FH∥AB,利用平行线的性质可得
首先作EG∥AB,FH∥AB,利用平行线的性质可得![]() ,再利用角平分线的定义得到
,再利用角平分线的定义得到![]() ,从而得到
,从而得到![]() 的度数;
的度数;
![]() 先由已知得到
先由已知得到![]() ,
,![]() , 由
, 由![]() 得
得![]()
![]() ,
,![]() , 等量代换,即可;
, 等量代换,即可;
![]() 由
由![]() 的方法可得到
的方法可得到![]() ,将
,将![]() 代入可得
代入可得![]() .
.
![]() 作EG∥AB, FH∥AB ,
作EG∥AB, FH∥AB ,
∵ AB∥CD ,
∴EG∥AB∥FH∥CD
,![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 和
和![]() 的角平分线相交于
的角平分线相交于![]() ,
,
![]() ,
,
![]() ;
;
![]()
![]()
![]()
![]()
![]() ,
,
![]() 与
与![]() 两个角的角平分线相交于
两个角的角平分线相交于![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() .
.
![]() 由
由![]() 结论可得,
结论可得,![]() ,
,![]() ,
,
解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在
 中,
中, 是
是 的中点,
的中点, 是
是 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 .
.(1)求证:
 ;
;(2)求证:四边形
 是菱形;
是菱形;(3)若
 ,求菱形
,求菱形 的面积.
的面积.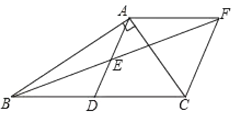
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,腰AB的垂直平分线DE交AB于点E,交AC于点D,且∠DBC=15°,则∠A的度数是 ( )

A.50°B.36°C.40°D.45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某天在南印度洋海域有两艘自西向东航行的搜救船A、B,B船在A船的正东方向,且两船保持40海里的距离.某一时刻两船同时测得在A的东北方向,B的北偏东15°方向有一疑似物C,求此时疑似物C与搜救船A、B的距离各是多少?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
相关试题

