【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).

(1)当t为________时,AD=AB,此时DE的长度为________;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>![]() 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
②当线段A′C′与射线BB1有公共点时,求t的取值范围.
参考答案:
【答案】(1)2,2;(2)t=6;(3)①S=12t2;② ![]() .
.
【解析】试题分析:(1)、根据Rt△ABC的勾股定理求出AB=10,根据AD=AB得出t的值,根据题意求出CD的长度,然后根据DE=CE-CD求出答案;(2)、首先根据题意得出四边形BCEF为矩形,分两种情况:当AD<AE时求出t的取值范围,然后根据△ACB和△DEF全等得出t的值;当AD>AE时求出t的取值范围,然后根据△ACB和△DEF全等得出t的值;(3)、根据题意得出△ABC和△ADH相似,从而得出AH=3t,DH=4t,从而得出函数解析式;当点A'落在射线BB1上的点B时,AA'=AB=10,根据AA'=2AH=2×5t×cos∠A得出t的值;当点C'落在射线BB1上时,四边形ACC'B为平行四边形,根据CC'=2CD×cos∠A求出t的值,从而得出t的取值范围.
试题解析:解:(1)在Rt△ABC中,AC=6,BC=8,根据勾股定理得,AB=![]() =10,
=10,
由运动知,AD=5t, ∵AD=AB, ∴5t=10, ∴t=2,
∴CD=AD﹣AC=10﹣6=4,CE=3t=6, ∴DE=CE﹣CD=2,
(2)、解:∵∠ACB=90°,BB1∥AC,EF⊥AC, ∴四边形BCEF是矩形,EF=BC=8,
当AD<AE时,5t<6+3t, ∴0<t<3,
若DE=AC,△ACB≌△DEF,DE=AE﹣AD=6+3t﹣5t=6﹣2t, ∴6﹣2t=6, ∴t=0,
∵t>0(不合题意,舍),
当AD>AE时,5t>6+3t, ∴t>3,
若DE=AC,△ACB≌△DEF,DE=AD﹣AE=5t﹣6﹣3t=2t﹣6,
∴2t﹣6=6, ∴t=6, ∴当t=6时,△DEF与△ACB全等.
(3)、解:①如图,
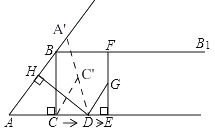
∵∠ACB=∠AHD,∠BAC=∠DAH, ∴△ABC∽△ADH, ∴![]() ,
,
∴![]() , ∴AH=3t,DH=4t, ∴S△ADA'=2S△ADH=2×
, ∴AH=3t,DH=4t, ∴S△ADA'=2S△ADH=2×![]() AH×DH=AH×DH=12t2 ,
AH×DH=AH×DH=12t2 ,
②当点A'落在射线BB1上的点B时,AA'=AB=10,
∵DH⊥AB, ∴AA'=2AH=2×5t×cos∠A=6t=10, ∴t=![]() ,
,
当点C'落在射线BB1上时,CC'∥AB, ∵BB1∥AC,∴四边形ACC'B为平行四边形,
∴CC'=AB=10, ∵CC'=2CD×cos∠A=2×(5t﹣6)×![]() =
=![]() (5t﹣6), ∴t=
(5t﹣6), ∴t=![]() ,
,
∴![]() ≤t≤
≤t≤![]() ,线段A'C'与射线BB1有公共点.
,线段A'C'与射线BB1有公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】背景情境:
赛赛同学在学习《一元二次方程》中做过这样一道题:
题目:已知实数
 、
、 满足
满足 ,
, ,且
,且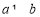 ,求
,求 的值.
的值.解:根据题意得
 与
与 为方程
为方程 的两根,
的两根,∴
 ,
,
∴

请认真阅读赛赛同学解题的方法,仔细思考.
解决问题:
(1)已知实数
 、
、 满足
满足 ,
, ,且
,且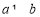 ,求
,求 的值.
的值.(2)设实数
 、
、 分别满足
分别满足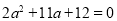 ,
, ,且
,且 ,求
,求 的值.
的值.(3)已知关于
 的方程
的方程 有两个根
有两个根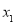 、
、 满足
满足 .当
.当 的三边
的三边 、
、 、
、 满足
满足 ,
, ,
, (a≠b).求
(a≠b).求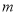 的值以及
的值以及 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=
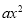 +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=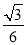 ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥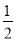 .正确的是( ).
.正确的是( ).A.①② B.③④ C.①②③ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村在开展“美丽乡村”建设中,决定购买
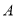 ,
,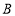 两种树苗对村里的主干道进行绿化改造,已知购买
两种树苗对村里的主干道进行绿化改造,已知购买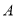 种树苗2棵,
种树苗2棵,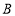 种树苗3棵,共需要260元;购买
种树苗3棵,共需要260元;购买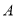 种树苗4棵,
种树苗4棵,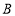 种树苗5棵,共需要480元.
种树苗5棵,共需要480元.(1)求购买
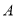 ,
, 两种树苗每棵各需多少元?
两种树苗每棵各需多少元?(2)该乡村现打算用不超过5000元的资金购买这两种树苗,问购买60棵
 种树苗后,至多还能购买多少棵
种树苗后,至多还能购买多少棵 种树苗?
种树苗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
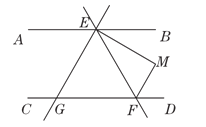
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
相关试题

