【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
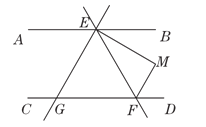
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
参考答案:
【答案】C
【解析】
根据角平分线的定义,平行线的性质和判定解答即可.
∵AB∥CD,∴∠DFE=∠AEF(两直线平行,内错角相等),①正确;
∵AB∥CD, ∴∠MFE+∠MEF=180°,
∵FM平分∠EFD,EM平分∠BEF,
∴∠MFE=![]() ∠DFE,∠MEF =
∠DFE,∠MEF =![]() ∠BEF,
∠BEF,
∴∠EMF=∠MFE+∠MEF = ![]() ∠DFE+
∠DFE+![]() ∠BEF=90°, ②正确;
∠BEF=90°, ②正确;
∵AB∥CD, ∴∠AEF=∠DFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=![]() ∠AEF,
∠AEF,
∵FM平分∠DFE,
∴∠EFM=∠MFD=![]() ∠DFE,
∠DFE,
∴∠GEF=∠EFM, ∴EG∥FM,③正确;
∵∠AEF=∠DFE≠∠EGC,④错误,正确的有3个,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).

(1)当t为________时,AD=AB,此时DE的长度为________;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>
 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;②当线段A′C′与射线BB1有公共点时,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=
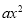 +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=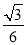 ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥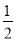 .正确的是( ).
.正确的是( ).A.①② B.③④ C.①②③ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村在开展“美丽乡村”建设中,决定购买
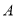 ,
,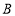 两种树苗对村里的主干道进行绿化改造,已知购买
两种树苗对村里的主干道进行绿化改造,已知购买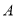 种树苗2棵,
种树苗2棵,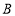 种树苗3棵,共需要260元;购买
种树苗3棵,共需要260元;购买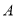 种树苗4棵,
种树苗4棵,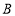 种树苗5棵,共需要480元.
种树苗5棵,共需要480元.(1)求购买
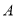 ,
,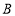 两种树苗每棵各需多少元?
两种树苗每棵各需多少元?(2)该乡村现打算用不超过5000元的资金购买这两种树苗,问购买60棵
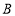 种树苗后,至多还能购买多少棵
种树苗后,至多还能购买多少棵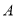 种树苗?
种树苗? -
科目: 来源: 题型:
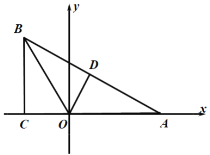
查看答案和解析>>【题目】如图,已知点
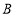 的坐标是
的坐标是 ,过
,过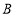 作
作 轴于
轴于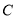 ,在
,在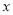 轴正半轴上截取
轴正半轴上截取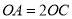 ,连接
,连接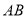 .
.
(1)求
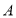 点的坐标及
点的坐标及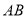 的解析式;
的解析式;(2)过
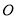 作
作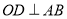 于
于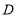 ,求证:
,求证: ;
;(3)
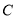 关于
关于 轴的对称点为
轴的对称点为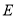 ,在
,在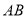 上取
上取 点,连接
点,连接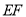 ,动点
,动点 沿
沿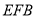 运动,
运动, 在
在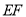 上的运动速度每秒1个单位长度,
上的运动速度每秒1个单位长度, 在
在 上运动速度每秒2个单位长度,当
上运动速度每秒2个单位长度,当 在何处时,
在何处时, 运动的时间最短?请求出
运动的时间最短?请求出 的坐标.
的坐标. -
科目: 来源: 题型:
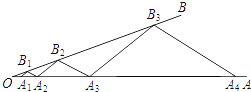
查看答案和解析>>【题目】如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 ,A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
相关试题

