【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
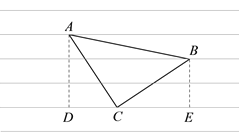
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

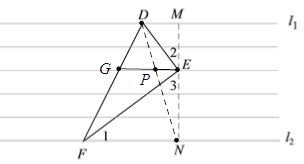
(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
参考答案:
【答案】AB=![]() ;
;
【解析】试题分析:(1)如图,过点A、B分别作点C所在横线的垂线,垂足分别为D、E,然后证明△ADC≌△CEB,从而可得CE=AD=3,CD=BE=2,由勾股定理求得AC,BC的长,再由勾股定理即可求得AB的长;
(2)如图所示,过点E作横线的垂线,然后证明△DME∽△ENF,再根据相似三角形的性质进行推导即可得;
(3)连接DN与EG交于点P,根据相似三角形的性质即可得.
试题解析:(1)过点A、B分别作点C所在横线的垂线,垂足分别为D、E,
∴∠ADC=∠BEC=90°,AD=3,BE=2,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∴∠DAC=∠ECB,
∵AC=BC,
∴△ADC≌△CEB,∴CE=AD=3,CD=BE=2,
∴AC=BC=![]() ,∴AB=
,∴AB=![]() ,
,
故答案为: ![]() ;
;
(2)过点E作横线的垂线,交l1,l2于点M,N,
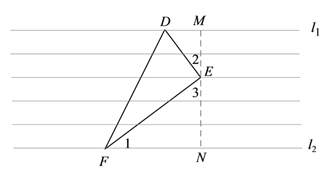
∴∠DME=∠EDF= 90°,
∵∠DEF=90°,
∴∠2+∠3=90°,
∵∠1+∠3=90°,
∴∠1=∠2,
∴△DME∽△ENF ,
∴![]() ,
,
∵EF=2DE,
∴![]() ,
,
∵ME=2,EN=3,
∴NF=4,DM=1.5,
根据勾股定理得DE=2.5,EF=5, ![]() ;
;
(3)连接DN,交EG于点P,
∵EG//DM,∴△DMN∽△PEN,
∴PE:DM=EN:MN,即PE:1.5=3:5,∴PE=0.9,
同理PG=1.6,∴EG=PE+PG=2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=
 , CF=3,求DF的长.
, CF=3,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=
 ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )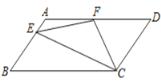
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 经过点A(-3,4).
经过点A(-3,4).(1)求b的值;
(2)过点A作
 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;①当点C恰巧落在
 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;②连结BC,求BC的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),点B(0,1)是第一个正方形OBB1C的两个顶点,以它的对角线OB1为一边作第二个正方形OB1B2C1,以正方形OB1B2C1的对角线OB2为一边作第三个正方形OB2B3C2,再以正方形OB2B3C2的对角线OB3为一边作第四个正方形OB3B4C3…以此规律作下去,点B2014的坐标为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1.

(1)在方格纸中画△ABC,使AB=
 ,AC=
,AC= ,BC=4;
,BC=4;(2)请你用所学的知识验证所画的△ABC是不是直角三角形.
相关试题

