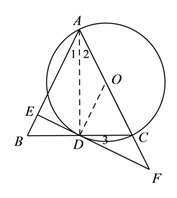
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

参考答案:
【答案】(1)见解析;(2)6
【解析】试题分析:连接OD,则有OD⊥EF,然后证明OD//AB即可得;
(2)连接AD,则有∠ADB=90°,通过证明△FCD∽△FDA ,可得 FC:FD=CD:DA,再根据tan∠BDE=![]() ,通过推导即可得.
,通过推导即可得.
试题解析:(1)连接OD.∵EF切⊙O于点D,∴OD⊥EF.
又∵OD=OC,∴∠ODC=∠OCD,
∵AB=AC,∴∠ABC=∠OCD,∴∠ABC=∠ODC,
∴AB∥OD,∴DE⊥AB;
(2)连接AD.
∵AC为⊙O的直径,∴∠ADB=90°, ∴∠B+∠BDE=90°,∠B+∠1=90°,
∴∠BDE=∠1,
∵AB=AC,∴∠1=∠2,又∵∠BDE =∠3,∴∠2=∠3,
∴△FCD∽△FDA ,∴ ![]() ,
,
∵tan∠BDE=![]() ,∴tan∠2=
,∴tan∠2=![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵CF=3,∴FD=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1) CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与
 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18,
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=
 ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )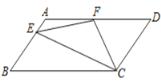
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
相关试题

