搜索
【题目】如图，点O（0,0），点B（0,1）是第一个正方形OBB1C的两个顶点，以它的对角线OB1为一边作第二个正方形OB1B2C1，以正方形OB1B2C1的对角线OB2为一边作第三个正方形OB2B3C2，再以正方形OB2B3C2的对角线OB3为一边作第四个正方形OB3B4C3…以此规律作下去，点B2014的坐标为______．
参考答案：
【答案】(-21007,0)
【解析】
根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以
，所以可求出从B到B3的后变化的坐标，再求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B2014的坐标．
根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以，
∵从B、B3经过了3次变化
∵
，
∴点B3所在的正方形的边长为
，点B3位置在第四象限
∴点B3的坐标是(2,2)
可得出：B1点坐标为(1,1)
B2点坐标为(0,2)
B3点坐标为(2,2)
B4点坐标为(0,4)
B5点坐标为(4,4)
B6(8,0)，B7(8,8)，B8(0,16)，B9(16,16)
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍
∵2014÷8=251…6
∴B2014的纵横坐标符号与点B6的相同，横坐标为负值，纵坐标为0
∴B2014的坐标为(21007,0)
故答案为：(21007,0)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：（1）∠DCF=
∠BCD；（2）EF=CF；（3）S△BEC= 2S△CEF；（4）∠DFE=3∠AEF；其中正确的结论是（ ）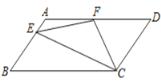
A.（1）（2）B.（1）（2）（4）C.（2）（3）（4）D.（1）（3）（4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．
（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB=__________；
（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；
（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线
经过点A（-3，4）．（1）求b的值；
（2）过点A作
轴的平行线交抛物线于另一点B，在直线AB上任取一点P，作点A关于直线OP的对称点C；①当点C恰巧落在
轴时，求直线OP的表达式；②连结BC，求BC的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，方格纸中每个小正方形的边长都是1．
（1）在方格纸中画△ABC，使AB=
，AC=
，BC=4；（2）请你用所学的知识验证所画的△ABC是不是直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD中，分别延长DC，BC至点E，F，使CE=CD，CF=CB，连接DB，BE，EF，FD．
（1）求证：四边形DBEF是矩形；
（2）如果∠A＝60°，DF的长为
，求菱形ABCD的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，再从中任意摸出1个球是白球的概率为
.（1）试求袋中蓝球的个数；
（2）第一次任意摸出一个球（不放回），第二次再摸出一个球，请用树状图或列表法表示两次摸到球的所有可能结果，并求两次摸到的球都是白球的概率.
相关试题
